题目内容
下列叙述正确的序号是
①对于定义在R上的函数f(x),若f(-3)=f(3),则函数f(x)不是奇函数;
②定义在R上的函数f(x),在区间(-∞,0]上是单调增函数,在区间(0,+∞)上也是单调增函数,则函数f(x)在R上是单调增函数;
③已知函数的解析式为y=x2,它的值域为{4,9},那么这样的函数有9个;
④对于任意的x1,x2∈(0,+∞),若函数f(x)=log2x,则
≤f(
).
①对于定义在R上的函数f(x),若f(-3)=f(3),则函数f(x)不是奇函数;
②定义在R上的函数f(x),在区间(-∞,0]上是单调增函数,在区间(0,+∞)上也是单调增函数,则函数f(x)在R上是单调增函数;
③已知函数的解析式为y=x2,它的值域为{4,9},那么这样的函数有9个;
④对于任意的x1,x2∈(0,+∞),若函数f(x)=log2x,则
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:分析:(1)根据奇函数的性质加以判断;
(2)不一定,可借助于数形结合加以判断;
(3)根据函数的三要素,只需确定其定义域的取值即可;
(4)这是考查函数凹凸性,也可以借助与图象判断.
(2)不一定,可借助于数形结合加以判断;
(3)根据函数的三要素,只需确定其定义域的取值即可;
(4)这是考查函数凹凸性,也可以借助与图象判断.
解答:
解:①由奇函数的定义可知,常数函数y=0,x∈R是奇函数,且满足f(-3)=f(3),所以①不对;
②如图是函数f(x)的图象,其满足在区间(-∞,0]上是单调增函数,在区间(0,+∞)上也是单调增函数,但不满足在R上是增函数,所以②错;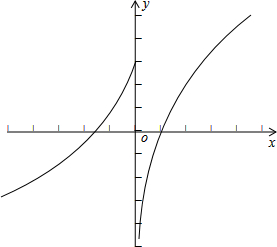
③令x2=4和x2=9得x=-2或2或-3或3.则定义域分别为{2,3}{2,-3}{-2,3}{-2,-3}{-2,2,3}{-2,2,-3}{-2,3,-3}{2,-3,3}{-2,2,-3,3}共9种情况,故③正确;
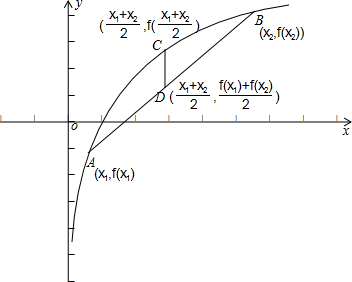
④如图,作出函数y=log2x的图象,从图中可以看出,
≤f(
),并且两点A、B重合时取等号,故④正确.
故答案为③④
②如图是函数f(x)的图象,其满足在区间(-∞,0]上是单调增函数,在区间(0,+∞)上也是单调增函数,但不满足在R上是增函数,所以②错;
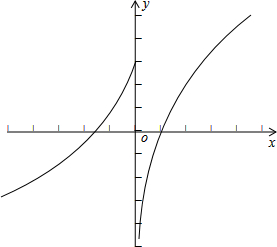
③令x2=4和x2=9得x=-2或2或-3或3.则定义域分别为{2,3}{2,-3}{-2,3}{-2,-3}{-2,2,3}{-2,2,-3}{-2,3,-3}{2,-3,3}{-2,2,-3,3}共9种情况,故③正确;
④如图,作出函数y=log2x的图象,从图中可以看出,
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |

故答案为③④
点评:这种类型的为题一般从概念出发来考虑,涉及函数的性质的问题,尤其是选择填空,一般采用数形结合的方法.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目