题目内容
已知
，
，
在同一平面内，且
=（-1，2）．
（1）若
=（m-1，3m），且
∥
，求m的值；
（2）若|
|=
，且（
+2
）⊥（2
-
），求向量
与
的夹角．
| a |
| b |
| c |
| a |
（1）若
| c |
| c |
| a |
（2）若|
| b |
| ||
| 2 |
| a |
| b |
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算,平面向量共线（平行）的坐标表示
专题：平面向量及应用
分析：（1）利用向量共线定理即可得出；
（2）利用向量垂直与数量积的关系即可得出．
（2）利用向量垂直与数量积的关系即可得出．
解答：
解：（1）由
∥
，得：2（m-1）+3m=0，解得 m=
．
（2）由(
+2
)⊥(2
-
)，得：(
+2
)•(2
-
)=0．
∴2
2+3
•
-2
2=0，
10+3
•
-
=0，
则
•
=-
．
|
||
|cosθ=-
，
×
cosθ=-
，cosθ=-1
向量
与
的夹角为π．
| c |
| a |
| 2 |
| 5 |
（2）由(
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴2
| a |
| a |
| b |
| b |
10+3
| a |
| b |
| 5 |
| 2 |
则
| a |
| b |
| 5 |
| 2 |
|
| a |
| b |
| 5 |
| 2 |
| 5 |
| ||
| 2 |
| 5 |
| 2 |
向量
| a |
| b |
点评：本题考查了向量共线定理、向量垂直与数量积的关系、向量的夹角，属于基础题．
练习册系列答案
相关题目
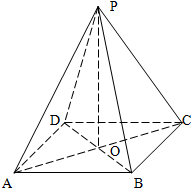如图，四棱锥P-ABCD的侧棱都相等，底面ABCD是正方形，O为对角线AC、BD的交点，PO=OA．