题目内容
11.考生甲填报某高校专业意向,打算从5个专业中挑选3个,分别作为第一、第二、第三志愿,则不同的填法有( )| A. | 10种 | B. | 60种 | C. | 125种 | D. | 243种 |
分析 从中选3个并分配到3个志愿中,问题得以解决.
解答 解:从中选3个并分配到3个志愿中,故有A53=60种,
故选:B.
点评 本题考查了简单的排列组合问题,关键是分清是排列还是组合,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知x,y满足$\left\{\begin{array}{l}{x+2y≤4}\\{x-y≤1}\\{x+2≥0}\end{array}\right.$,目标函数z=1-2x-y的最大值为a,最小值为b,则a-b=( )
| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
6.若函数f(x)=2sin2x的图象向右平移φ(0<φ<π)个单位后得到函数g(x)的图象,若对满足|f(x1)-g(x2)|=4的x1、x2,有|x1-x2|的最小值为$\frac{π}{6}$,则φ=( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{6}$或$\frac{5π}{6}$ |
20.(2x+5y)2016展开式中第k+1项的系数为( )
| A. | $C_{2016}^k{2^{2016-k}}{5^{k-1}}$ | B. | $C_{2016}^{k-1}{2^{2017-k}}{5^{k-1}}$ | ||
| C. | $C_{2016}^{k-1}$ | D. | $C_{2016}^k{2^{2016-k}}{5^k}$ |
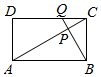 如图,在矩形ABCD中,AB=$\sqrt{3}$AD,点Q为线段CD(含端点)上一个动点,且$\overrightarrow{DQ}$=λ$\overrightarrow{QC}$,BQ交AC于P,且$\overrightarrow{AP}$=μ$\overrightarrow{PC}$,若AC⊥BP,则λ-μ=-1.
如图,在矩形ABCD中,AB=$\sqrt{3}$AD,点Q为线段CD(含端点)上一个动点,且$\overrightarrow{DQ}$=λ$\overrightarrow{QC}$,BQ交AC于P,且$\overrightarrow{AP}$=μ$\overrightarrow{PC}$,若AC⊥BP,则λ-μ=-1.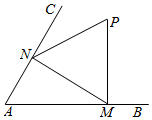 如图,已知∠BAC=$\frac{π}{3}$,正△PMN的顶点M、N分别在射线AB、AC上运动,P在∠BAC的内部,MN=2,M、P、N按逆时针方向排列,设∠AMN=θ.
如图,已知∠BAC=$\frac{π}{3}$,正△PMN的顶点M、N分别在射线AB、AC上运动,P在∠BAC的内部,MN=2,M、P、N按逆时针方向排列,设∠AMN=θ.