题目内容
19.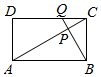 如图,在矩形ABCD中,AB=$\sqrt{3}$AD,点Q为线段CD(含端点)上一个动点,且$\overrightarrow{DQ}$=λ$\overrightarrow{QC}$,BQ交AC于P,且$\overrightarrow{AP}$=μ$\overrightarrow{PC}$,若AC⊥BP,则λ-μ=-1.
如图,在矩形ABCD中,AB=$\sqrt{3}$AD,点Q为线段CD(含端点)上一个动点,且$\overrightarrow{DQ}$=λ$\overrightarrow{QC}$,BQ交AC于P,且$\overrightarrow{AP}$=μ$\overrightarrow{PC}$,若AC⊥BP,则λ-μ=-1.
分析 可由$\overrightarrow{DQ}=λ\overrightarrow{QC}$得到$\overrightarrow{DC}=(λ+1)\overrightarrow{QC}$,从而便可得到$\frac{AB}{QC}=λ+1$,而同理可以由$\overrightarrow{AP}=μ\overrightarrow{PC}$可以得出$\frac{AP}{PC}=μ$,而△PAB和△PCQ相似,从而根据相似三角形对应边的比例关系便可得出λ+1=μ,从而可得出λ-μ的值.
解答 解:$\overrightarrow{DQ}=λ\overrightarrow{QC}$;
∴$\overrightarrow{DC}=(λ+1)\overrightarrow{QC}$;
∴AB=DC=(λ+1)QC;
∴$\frac{AB}{QC}=λ+1$;
∵$\overrightarrow{AP}=μ\overrightarrow{PC}$;
∴AP=μPC;
∴$\frac{AP}{PC}=μ$;
又△PCQ∽△PAB;
∴$\frac{AB}{QC}=\frac{AP}{PC}$;
∴λ+1=μ;
∴λ-μ=-1.
故答案为:-1.
点评 考查向量数乘的几何意义,以及三角形相似的概念,相似三角形对应边的比例关系.

练习册系列答案
相关题目
14.定义在R上的函数f(x)=$\frac{xsin2x}{{x}^{2}+a}$的图象如图所示,则实数a的可能值为( )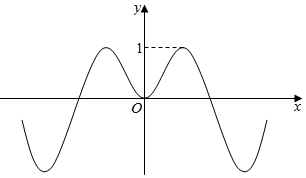

| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
4.已知$tan(α+\frac{π}{4})=2$,则tan2α=( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{3}{5}$ |
11.考生甲填报某高校专业意向,打算从5个专业中挑选3个,分别作为第一、第二、第三志愿,则不同的填法有( )
| A. | 10种 | B. | 60种 | C. | 125种 | D. | 243种 |
8.已知sin(π-α)=-2sin($\frac{π}{2}$+α),则tanα的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |



