题目内容
16.已知x,y满足$\left\{\begin{array}{l}{x+2y≤4}\\{x-y≤1}\\{x+2≥0}\end{array}\right.$,目标函数z=1-2x-y的最大值为a,最小值为b,则a-b=( )| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义进行求解即可.
解答 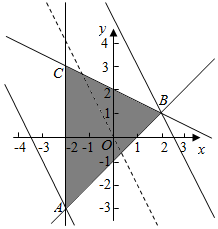 解:作出不等式组对应的平面区域如图,
解:作出不等式组对应的平面区域如图,
由z=1-2x-y得y=1-2x-z,
平移直线y=1-2x-z,当直线y=1-2x-z经过点B时,直线y=1-2x-z的截距最大,此时z最小,
由$\left\{\begin{array}{l}{x+2y=4}\\{x-y=1}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,即B(2,1),此时b=z=1-4-1=-4,
当直线y=1-2x-z经过点A时,直线y=1-2x-z的截距最小,此时z最大,
由$\left\{\begin{array}{l}{x=-2}\\{x-y=1}\end{array}\right.$得$\left\{\begin{array}{l}{x=-2}\\{y=-3}\end{array}\right.$,即A(-2,-3),此时a=z=1+4+3=8,
则a-b=8-(-4)=8+4=12,
故选:B
点评 本题主要考查线性规划的应用,根据利用数形结合求出目标函数的最值是解决本题的关键.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
6.若函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0),满足f(0)=f($\frac{π}{3}$),且函数在[0,$\frac{π}{2}$]上有且只有一个零点,则f(x)的最小正周期为( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
7.集合A={x|x2-x-2=0},B={x|x2+x+m=0},若A∩B≠∅,则m的值为( )
| A. | -6或6 | B. | 0或6 | C. | 0或-6 | D. | 0或±6 |
11.等差数列{an}中,已知通项公式an=3n-2,则S20=( )
| A. | 390 | B. | 590 | C. | 780 | D. | 295 |
8.已知A,B是锐角三角形的两个内角,则复数(sinA-cosB)+(sinB-cosA)i在复平面内对应的点位于( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
11.考生甲填报某高校专业意向,打算从5个专业中挑选3个,分别作为第一、第二、第三志愿,则不同的填法有( )
| A. | 10种 | B. | 60种 | C. | 125种 | D. | 243种 |