题目内容
6.若函数f(x)=2sin2x的图象向右平移φ(0<φ<π)个单位后得到函数g(x)的图象,若对满足|f(x1)-g(x2)|=4的x1、x2,有|x1-x2|的最小值为$\frac{π}{6}$,则φ=( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{6}$或$\frac{5π}{6}$ |
分析 利用三角函数的最值,求出自变量x1,x2的值,然后判断选项即可得解.
解答 解:因为将函数f(x)=2sin2x的周期为π,函数的图象向右平移φ(0<φ<π)个单位后得到函数g(x)的图象.若对满足|f(x1)-g(x2)|=4的可知,两个函数的最大值与最小值的差为4,有|x1-x2|min=$\frac{π}{6}$,
不妨x1=$\frac{π}{4}$,x2=$\frac{π}{12}$,即g(x)在x2=$\frac{π}{12}$,取得最小值,sin(2×$\frac{π}{12}$-2φ)=-1,
此时φ=$\frac{π}{3}$-kπ,k∈Z,结合0<φ<π,可得φ=$\frac{π}{3}$,满足题意.
x1=$\frac{π}{4}$,x2=$\frac{5π}{12}$,即g(x)在x2=$\frac{5π}{12}$,取得最小值,sin(2×$\frac{5π}{12}$-2φ)=-1,
此时φ=$\frac{2π}{3}$-kπ,k∈Z,结合0<φ<π,可得φ=$\frac{2π}{3}$,满足题意.
故选:C.
点评 本题主要考查了三角函数的图象平移,函数的最值以及函数的周期的应用,考查分析问题解决问题的能力,是好题,题目新颖.有一定难度,选择题,可以回代验证的方法快速解答,属于中档题.

练习册系列答案
相关题目
11.等差数列{an}中,已知通项公式an=3n-2,则S20=( )
| A. | 390 | B. | 590 | C. | 780 | D. | 295 |
14.定义在R上的函数f(x)=$\frac{xsin2x}{{x}^{2}+a}$的图象如图所示,则实数a的可能值为( )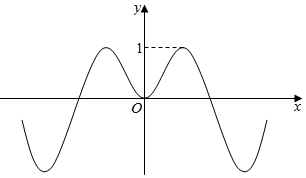

| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
11.考生甲填报某高校专业意向,打算从5个专业中挑选3个,分别作为第一、第二、第三志愿,则不同的填法有( )
| A. | 10种 | B. | 60种 | C. | 125种 | D. | 243种 |
15.已知集合A={x|x-1|≤2},B={x|0<x<2},则A∪B=( )
| A. | A | B. | B | C. | ∅ | D. | R |