题目内容
已知数列{an}是等比数列，且a3-a1=8，a6-a4=216，Sn=40，求公比q，a1，及n．
考点：等比数列的前n项和,等比数列的通项公式
专题：等差数列与等比数列
分析：由题意可得首项和公比的方程组，解方程组可得q，a1，再由求和公式可得n的方程，解之可得．
解答：
解：∵数列{an}是等比数列，设an=a1qn-1，
由题意可得
，代入数据可得
，
解得a1=1，q=3，
∴Sn=
=
=40，解得n=4
由题意可得
|
|
解得a1=1，q=3，
∴Sn=
| a1(1-qn) |
| 1-q |
| 1-3n |
| 1-3 |
点评：本题考查等等比数列的通项公式和求和公式，属基础题．
练习册系列答案
相关题目
若
=3，则
=（ ）
| sin(α+β) |
| sin(β-α) |
| tanα |
| tanβ |
A、
| ||
B、
| ||
C、
| ||
D、
|
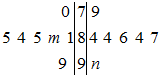如图是2010年“唱响九江”电视歌手大奖赛中，七位专家评委为甲、乙两名选手打出的分数的茎叶图（其中m，n为数字0～9中的一个），去掉一个最高分和一个最低分后，甲、乙两名选手得分的平均数分别为a1，a2，则一定有（ ）| A、a1＞a2 |
| B、a2＞a1 |
| C、a1，a2的大小与m的值有关 |
| D、a1，a2的大小与m，n的值都有关 |
若x1，x2是方程lg2x+（lg3+lg2）lgx+lg3•lg2=0的两根，则x1x2的值是（ ）
A、
| ||
| B、lg6 | ||
| C、6 | ||
| D、lg3•lg2 |
若函数f（x）是定义在R上的偶函数，在（-∞，0）上是减函数，且f（2）=0，则不等式x•f（x）＜0的解集是（ ）
| A、（-∞，-2）∪（2，+∞） |
| B、（-2，2） |
| C、（-∞，-2）∪（0，2） |
| D、（-2，0）∪（2，+∞） |