题目内容

求和2+2×22+3×23+4×24+5×25+6×26+7×27=
 
．
考点：数列的求和
专题：等差数列与等比数列
分析：利用错位相减法能求出结果．
解答： 解：设S7=2+2×22+3×23+4×24+5×25+6×26+7×27，①
2S7=22+2×23+3×24+4×25+5×26+6×27+7×28，②
①-②，得：
-S7=2+22+23+24+25+26+27-7×28
=
2(1-27)
1-2
-7×28
=-6×28-2
=-1358，
∴S7=1358．
故答案为：1358．
点评：本题考查数列的前n项和的求法，是中档题，解题时要注意错位相减法的合理运用．
练习册系列答案
相关题目
已知函数f（x）=cos（2x-
π
3
）-2cos（x+
π
4
）sin（x+
π
4
）
（1）求函数f（x）的最小正周期和图象的对称轴；
（2）求函数f（x）在区间[-
π
12
，
π
2
]上的值域．
设不等式组
0≤x≤1
0≤y≤2
表示的平面区域为M，若随机向M内投入一点，则该点到（1，2）的距离大于1的概率为（　　）
A、
π
4
B、
π
8
C、
4-π
4
D、
8-π
8
计算：
tan22.5°
1-tan222.5°
=
 
．
已知函数f（x）是定义在R上的奇函数．
（1）请把f（x）解析式填写完整f（x）=
x(2-x)(x≥0)
()(x＜0)

（1）画出函数f（x）的简图；
（3）若g（x）=a，F（x）=f（x）-g（x），当a在
 
范围F（x）有且只有一个零点．
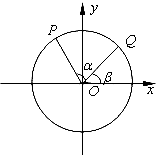如图，以ox轴为始边作角α与β（0＜β＜α＜π），它们终边分别与单位圆相交于点P，Q，已知点P的坐标为（-
3
5
，
4
5
）
（1）求
sin2α+cos2α+1
1+tanα
的值；
（2）若OP⊥OQ，求
sin(α+β)
2
cos(
π
4
+β)
．
已知函数f（x）=2sin
x
4
cos
x
4
-2
3
sin2
x
4
+
3
，且g(x)=f(x+
π
3
)．
（1）判断g（x）的奇偶性
（2）求g（x）的单调递增区间．
已知数列{an}的前n项和Sn=n3，则a4=（　　）
A、37B、27C、64D、91
已知数列{an}是等比数列，且a3-a1=8，a6-a4=216，Sn=40，求公比q，a1，及n．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网