题目内容
1.要得到函数y=cos(2x-$\frac{π}{3}$)图象,只需将函数y=sin($\frac{π}{2}$+2x)图象( )| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
分析 根据三角函数的图象关系进行化简求解即可.
解答 解:$y=sin(\frac{π}{2}+2x)$=cos2x,
∵$y=cos(2x-\frac{π}{3})$=cos2(x-$\frac{π}{6}$),
∴需将函数$y=sin(\frac{π}{2}+2x)$图象向右平移$\frac{π}{6}$个单位即可得到$y=cos(2x-\frac{π}{3})$,
故选:D
点评 本题主要考查三角函数图象关系的判断,比较基础.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为2,则渐近线方程为( )
| A. | y=±2x | B. | y=±$\frac{\sqrt{3}}{3}$x | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{1}{2}$x |
16.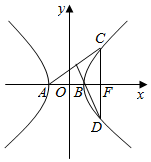 如图所示,双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,左、右顶点为A,B过F作x轴的垂线与双曲线交于C,D两点,若AC⊥BD,则该双曲线的离心率等于( )
如图所示,双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,左、右顶点为A,B过F作x轴的垂线与双曲线交于C,D两点,若AC⊥BD,则该双曲线的离心率等于( )
 如图所示,双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,左、右顶点为A,B过F作x轴的垂线与双曲线交于C,D两点,若AC⊥BD,则该双曲线的离心率等于( )
如图所示,双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,左、右顶点为A,B过F作x轴的垂线与双曲线交于C,D两点,若AC⊥BD,则该双曲线的离心率等于( )| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
10.已知O为坐标原点,双曲线$C:\frac{x^2}{a^2}-{y^2}=1(a>0)$上有一点P,过点P作双曲线C的两条渐近线的平行线,与两渐近线的交点分别为A,B,若平行四边形OAPB的面积为1,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{{\sqrt{5}}}{2}$ |