题目内容
6.在△ABC中存在一点O,满足∠BAO=∠CAO=∠CBO=∠ACO.求证:AB2=BC•AC.分析 根据已知条件∠BAO=∠CAO=∠CBO=∠ACO=$\frac{1}{2}$∠BAC,得到OA=OC,
设∠BAC=α,∠ABC=β,∠ACB=γ,由正弦定理得:$\frac{OA}{sin(β-\frac{1}{2}α)}=\frac{BO}{sin\frac{1}{2}α}$,$\frac{CO}{sin\frac{1}{2}α}=\frac{BO}{sin(γ-\frac{1}{2}α)}$,两列相比得到:$si{n}^{2}\frac{1}{2}α$=sin(β-$\frac{1}{2}$α)•sin(γ-$\frac{1}{2}$α),化简后即可得到结论.
解答 证明:根据已知条件∠BAO=∠CAO=∠CBO=∠ACO=$\frac{1}{2}$∠BAC,
∴OA=OC,
设∠BAC=α,∠ABC=β,∠ACB=γ,
由正弦定理得:$\frac{OA}{sin(β-\frac{1}{2}α)}=\frac{BO}{sin\frac{1}{2}α}$,
$\frac{CO}{sin\frac{1}{2}α}=\frac{BO}{sin(γ-\frac{1}{2}α)}$,
两列相比得到:$si{n}^{2}\frac{1}{2}α$=sin(β-$\frac{1}{2}$α)•sin(γ-$\frac{1}{2}$α),
∴1-cosα=cos(β-γ)-cos(β+γ-α),1+cos(β+γ-α)=cos(β-γ)+cosα.
∵β+γ-α=180°-2α,
∴2sin2α=2sinβsinγ,
∴BC2=AC•AB.
点评 本题考查了三角形的内角和,正弦定理,三角函数,正确掌握正弦定理是解题的关键.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程为y=$\frac{\sqrt{6}}{6}$x,则此双曲线的离心率为( )
| A. | $\frac{\sqrt{42}}{6}$ | B. | $\frac{7}{6}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{5}{4}$ |
1.要得到函数y=cos(2x-$\frac{π}{3}$)图象,只需将函数y=sin($\frac{π}{2}$+2x)图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
18.如图所示的数阵中,用A(m,n)表示第m行的第n个数,则依此规律A(8,2)为( )
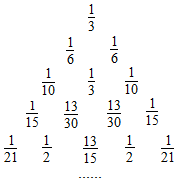

| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{7}{12}$ | D. | $\frac{11}{18}$ |
16.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的渐近线截圆(x-2)2+y2=3所得的弦长等于2$\sqrt{2}$,则双曲线的离心率为( )
| A. | 2 | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{5}$ |