将甲乙等5名交警分配到三个不同的路口疏通交通.每个路口至少一人.且甲乙在同一路口的分配方案有36种．题目和参考答案——青夏教育精英家教网—

题目内容

11．将甲乙等5名交警分配到三个不同的路口疏通交通，每个路口至少一人，且甲乙在同一路口的分配方案有36种．

分析通过将甲乙两人看做一个整体，相当于将4名交警分配到三个不同的路口疏通交通，每个路口至少一人，再将其中任意2名看做一人，即将三名交警分配到三个不同的路口，利用排列数公式计算即得结论．

解答解：依题意，将甲乙两人看做一个整体，
则相当于将4名交警分配到三个不同的路口疏通交通，每个路口至少一人，
故满足题意的方案有${C}_{4}^{2}$${A}_{3}^{3}$=36种，
故答案为：36．

点评本题考查排列、组合的实际应用，考查分析问题、解决问题的能力，注意解题方法的积累，属于中档题．

练习册系列答案

	A．	向左平移$\frac{π}{3}$个单位		B．	向右平移$\frac{π}{3}$个单位
	C．	向左平移$\frac{π}{6}$个单位		D．	向右平移$\frac{π}{6}$个单位

2．下列函数中，x=0是极值点的函数是（　　）

19．双曲线${x^2}-\frac{y^2}{3}=1$的离心率为（　　）

6．当φ=$\frac{π}{2}$，$\frac{3π}{2}$时，求出渐开线$\left\{\begin{array}{l}{x=cosφ+φsinφ}\\{y=sinφ-φcosφ}\end{array}\right.$上的对应点A，B，并求出点A，B间的距离．

16．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的渐近线截圆（x-2）²+y²=3所得的弦长等于2$\sqrt{2}$，则双曲线的离心率为（　　）

A．

B．

$\frac{{2\sqrt{3}}}{3}$

C．

$\frac{{\sqrt{5}}}{2}$

D．

$\sqrt{5}$

3．在极坐标系中，曲线C₁的极坐标方程为ρ=2cosθ+2sinθ，以极点为原点，极轴为x轴的正半轴，取与极坐标相同单位长度，建立平面直角坐标系，曲线C₂的参数方程为$\left\{\begin{array}{l}{x=2+cosa}\\{y=sina}\end{array}\right.$（a为参数）．
（1）求曲线C₁的平面直角坐标方程和曲线C₂的极坐标方程；
（2）点P是曲线C₂上一动点，求点P到直线ρsin（θ-$\frac{π}{3}$）=3的最小距离．

1．

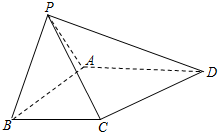如图，在四棱锥P-ABCD中，锐角三角形PAB所在的平面与底面ABCD垂直，∠PBC=∠BAD=90°．
（1）求证：BC⊥平面PAB；
（2）求证：AD∥平面PBC．

试题分类