题目内容
9.双曲线$M:{x^2}-\frac{y^2}{b^2}=1$的左,右焦点分别为F1,F2,记|F1F2|=2c,以坐标原点O为圆心,c为半径的圆与双曲线M在第一象限的交点为P,若|PF1|=c+2,则P点的横坐标为$\frac{\sqrt{3}+1}{2}$.分析 求得圆O的方程,联立双曲线的方程,求得P的横坐标,再由双曲线的定义,和直角三角形的勾股定理,可得c,b,化简整理可得所求横坐标的值.
解答 解:坐标原点O为圆心,c为半径的圆的方程为x2+y2=c2,
由$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}={c}^{2}}\\{{x}^{2}-\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,解得x2=$\frac{{c}^{2}+{b}^{2}}{{b}^{2}+1}$,
由|PF1|=c+2,
由双曲线的定义可得|PF2|=|PF1|-2a=c+2-2=c,
在直角三角形PF1F2中,可得c2+(c+2)2=4c2,
解得c=1+$\sqrt{3}$,
由c2=a2+b2=1+b2,可得b2=3+2$\sqrt{3}$,
可得P的横坐标为$\sqrt{\frac{7+4\sqrt{3}}{4+2\sqrt{3}}}$=$\frac{1+\sqrt{3}}{2}$.
故答案为:$\frac{{\sqrt{3}+1}}{2}$.
点评 本题考查双曲线的定义、方程和性质,考查直径所对的圆周角为直角,以及勾股定理的运用,考查化简整理的运算能力,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
20.双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1的渐近线方程与圆(x-$\sqrt{3}$)2+(y-1)2=1相切,则此双曲线的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程为y=$\frac{\sqrt{6}}{6}$x,则此双曲线的离心率为( )
| A. | $\frac{\sqrt{42}}{6}$ | B. | $\frac{7}{6}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{5}{4}$ |
4.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与抛物线x2=y-1只有一个公共点,则双曲线的离心率为( )
| A. | 5 | B. | $\frac{5}{4}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
1.要得到函数y=cos(2x-$\frac{π}{3}$)图象,只需将函数y=sin($\frac{π}{2}$+2x)图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
18.如图所示的数阵中,用A(m,n)表示第m行的第n个数,则依此规律A(8,2)为( )
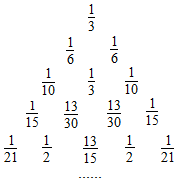

| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{7}{12}$ | D. | $\frac{11}{18}$ |
19.双曲线${x^2}-\frac{y^2}{3}=1$的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |