题目内容
16．
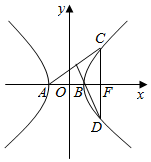如图所示，双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F，左、右顶点为A，B过F作x轴的垂线与双曲线交于C，D两点，若AC⊥BD，则该双曲线的离心率等于（ ）| A． | 3 | B． | 2 | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |
分析 求出A，B的坐标，令x=c代入双曲线的方程可得C，D的坐标，运用两直线垂直的条件：斜率之积为-1，化简可得a=b，求得c，由离心率公式计算即可得到所求值．
解答 解：由题意可得A（-a，0），B（a，0），
令x=c，则y=±b$\sqrt{\frac{{c}^{2}}{{a}^{2}}-1}$=±$\frac{{b}^{2}}{a}$，
可得C（c，$\frac{{b}^{2}}{a}$），D（c，-$\frac{{b}^{2}}{a}$），
由AC⊥BD，可得kAC•kBD=-1，
即有$\frac{\frac{{b}^{2}}{a}}{c+a}$•$\frac{-\frac{{b}^{2}}{a}}{c-a}$=-1，
化简可得$\frac{{b}^{4}}{{a}^{2}}$=c2-a2=b2，
即有a=b，c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{2}$a，
可得e=$\frac{c}{a}$=$\sqrt{2}$．
故选：D．
点评 本题考查双曲线的离心率的求法，注意运用两直线垂直的条件：斜率之积为-1，考查化简整理的运算能力，属于基础题．
练习册系列答案
相关题目
16．在△ABC中，∠C=90°，AC=2，点M满足$\overrightarrow{BM}$=$\overrightarrow{MA}$，则$\overrightarrow{CM}$•$\overrightarrow{CA}$=（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
4．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线与抛物线x2=y-1只有一个公共点，则双曲线的离心率为（ ）
| A． | 5 | B． | $\frac{5}{4}$ | C． | $\sqrt{5}$ | D． | $\frac{\sqrt{5}}{2}$ |
11．已知圆C的圆心与双曲线4x2-$\frac{4}{3}{y^2}$=1的左焦点重合，又直线4x-3y-6=0与圆C相切，则圆C的标准方程为（ ）
| A． | （x-1）2+y2=4 | B． | （x+1）2+y2=2 | C． | （x+1）2+y2=1 | D． | （x+1）2+y2=4 |
1．要得到函数y=cos（2x-$\frac{π}{3}$）图象，只需将函数y=sin（$\frac{π}{2}$+2x）图象（ ）
| A． | 向左平移$\frac{π}{3}$个单位 | B． | 向右平移$\frac{π}{3}$个单位 | ||
| C． | 向左平移$\frac{π}{6}$个单位 | D． | 向右平移$\frac{π}{6}$个单位 |
8．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线的斜率为-2，则C的离心率e=（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | 2 | D． | $\sqrt{5}$ |
5．设F1，F2分别是双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点，若双曲线右支上存在一点P，使得（${\overrightarrow{OP}$+$\overrightarrow{O{F_2}}}$）•$\overrightarrow{{F_2}P}$=0，其中O为坐标原点，且|${\overrightarrow{P{F_1}}}$|=2|${\overrightarrow{P{F_2}}}$|，则该双曲线的离心率为（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\sqrt{3}$+1 | C． | $\frac{\sqrt{5}}{2}$ | D． | $\sqrt{5}$ |