题目内容
函数f(x)=x2-mx+4(m>0﹚在(-∞,0]上的最小值是 .
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:由条件利用二次函数的性质可得判断函数f(x)在(-∞,0]上是减函数,从而求得函数的最小值.
解答:
解:∵函数f(x)=x2-mx+4=(x-
)2+4-
,(m>0﹚
∴函数f(x)=x2-mx+4(m>0﹚在(-∞,0]上是减函数,
故当x=0时,函数f(x)取得最小值为f(0)=4,
故答案为:4.
| m |
| 2 |
| m2 |
| 4 |
∴函数f(x)=x2-mx+4(m>0﹚在(-∞,0]上是减函数,
故当x=0时,函数f(x)取得最小值为f(0)=4,
故答案为:4.
点评:本题主要考查二次函数的性质的应用,判断函数f(x)在(-∞,0]上是减函数,是解题的关键,属于基础题.

练习册系列答案
相关题目
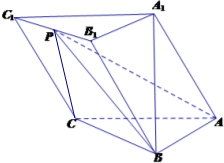 如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.
如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.