题目内容
设变量x,y满足约束条件
.若目标函数z=ax+y在点(1,2)处取得最大值,则a的取值范围为( )
|
| A、(1,+∞) |
| B、(-∞,-1) |
| C、(-1,1) |
| D、[-1,1] |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式对应的平面区域,利用线性规划的知识,确定目标取最优解的条件,即可求出a的取值范围.
解答:
解:作出不等式对应的平面区域,
由z=ax+y得y=-ax+z,
要使目标函数z=ax+y仅在点A(1,2)处取得最大值,
若a>0,此时目标函数的斜率k=-a<0,
则此时-a≤-1,即a>1,
若a<0,则-a>0,此时不满足条件,
故选:A
由z=ax+y得y=-ax+z,

要使目标函数z=ax+y仅在点A(1,2)处取得最大值,
若a>0,此时目标函数的斜率k=-a<0,
则此时-a≤-1,即a>1,
若a<0,则-a>0,此时不满足条件,
故选:A
点评:本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.根据条件目标函数z=ax+y仅在点A(1,2)处取得最大值,确定直线的位置是解决本题的关键.

练习册系列答案
相关题目
下列集合中为空集的是( )
| A、{x∈N|x2≤0} |
| B、{x∈R|x2-1=0} |
| C、{x∈R|x2+x+1=0} |
| D、{0} |
甲、乙两人数学成绩的茎叶图,如图所示,则两人的成绩中位数为( )


| A、87,98 |
| B、98,87 |
| C、88,88 |
| D、81,83 |
若集合M={y|y=3x},集合S={x|y=lg(x-1)},则下列各式正确的是( )
| A、M∪S=M | B、M∪S=S |
| C、M=S | D、M∩S=∅ |
f(x)是偶函数,定义域是(-∞,+∞),在[0,+∞)上f(x)是减函数,那么f(-
)与f(a2-a+1)(a∈R)的大小关系是( )
| 3 |
| 4 |
A、f(-
| ||
B、f(-
| ||
C、f(-
| ||
D、f(-
|
有两个等差数列{an},{bn},它们的前n项和分别为Sn,Tn,若
=
,则
=( )
| an |
| bn |
| 4n+3 |
| n+2 |
| S11 |
| T11 |
A、
| ||
B、
| ||
C、
| ||
D、
|
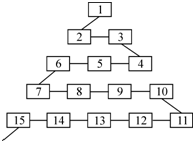 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;…;依此类推,则
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;…;依此类推,则