题目内容
设向量
，
的夹角θ定义：
×
=|
||
|sinθ 若平面内互不相等的两个非零向量
，
满足：|
|=1，（
-
）与
的夹角为150°，
×
的最大值为（ ）
| α |
| β |
| α |
| β |
| α |
| β |
| a |
| b |
| a |
| a |
| b |
| b |
| a |
| b |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
考点：平面向量数量积的运算
专题：计算题,解三角形,平面向量及应用
分析：设
=
，
=
，则
=
-
，由已知可得：B点为半径为1的圆上与OA不重合的动点，运用正弦定理和三角函数的化简，以及余弦函数的最值，可得答案．
| a |
| OA |
| b |
| OB |
| BA |
| a |
| b |
解答：
解：设
=
，
=
，
则
=
-
，
∵|
|=1，
-
与
的夹角为150°，
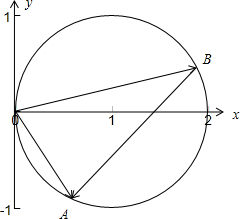
∴△OAB中，OA=1，∠OBA=30°，
由正弦定理可得：△OAB的半径为1，
则B点为圆上与OA不重合的动点，
设∠AOB=θ（0°＜θ＜150°），
由正弦定理可得，AB=2sinθ，OB=2sin（150°-θ），
则
×
=OA•OBsinθ=2S△OAB=AB•OB•sin30°
=2sinθsin（150°-θ）=-[cos150°-cos（2θ-150°）]
=
+cos（2θ-150°），
当θ=75°时，
×
取得最大值，且为1+
．
故选C．
解：设| a |
| OA |
| b |
| OB |
则
| BA |
| a |
| b |
∵|
| a |
| a |
| b |
| b |
∴△OAB中，OA=1，∠OBA=30°，
由正弦定理可得：△OAB的半径为1，
则B点为圆上与OA不重合的动点，
设∠AOB=θ（0°＜θ＜150°），
由正弦定理可得，AB=2sinθ，OB=2sin（150°-θ），
则
| a |
| b |
=2sinθsin（150°-θ）=-[cos150°-cos（2θ-150°）]
=
| ||
| 2 |
当θ=75°时，
| a |
| b |
| ||
| 2 |
故选C．
点评：本题考查的知识点是平面向量的夹角概念，余弦函数的图象和性质，是三角函数与向量的综合应用，难度中档．
练习册系列答案
相关题目
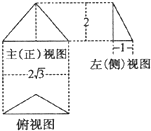已知一个三棱锥的三视图如图所示，其中俯视图是顶角为120°的等腰三角形，则该三棱锥的四个表面中，面积的最大值为