题目内容
已知函数f（x）=
的定义域为[2，3]，则实数m的值为（ ）
| -x2+mx-6 |
| A、5 | B、-5 | C、10 | D、-10 |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：把函数f（x）=
的定义域为[2，3]，转化为方程x2-mx+6=0的两个根为2，3，然后由根与系数关系得答案．
| -x2+mx-6 |
解答：
解：∵函数f（x）=
的定义域为[2，3]，
即不等式-x2+mx-6≥0的解集为[2，3]，
也就是方程x2-mx+6=0的两个根为2，3．
由根与系数关系得m=2+3=5．
∴实数m的值为5．
故选：A．
| -x2+mx-6 |
即不等式-x2+mx-6≥0的解集为[2，3]，
也就是方程x2-mx+6=0的两个根为2，3．
由根与系数关系得m=2+3=5．
∴实数m的值为5．
故选：A．
点评：本题考查了函数的定义域及其求法，考查了数学转化思想方法，是基础题．
练习册系列答案
相关题目
b＞0是函数f（x）=x2+bx+c在[0，+∞）单调的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
命题“对任意的x∈R，都有2x2-x+1≥0”的否定是（ ）
| A、对任意的x∈R，都有2x2-x+1＜0 |
| B、存在x0∈R，使得2x02-x0+1＜0 |
| C、不存在x0∈R，使得2x02-x0+1＜0 |
| D、存在x0∈R，使得2x02-x0+1≥0 |
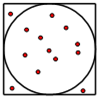某同学动手做实验：《用随机模拟的方法估计圆周率的值》，在如图的正方形中随机撒豆子，每个豆子落在正方形内任何一点是等可能的，若他随机地撒50粒统计得到落在圆内的豆子数为39粒，则由此估计出的圆周率π的值为