题目内容
16.双曲线$C:\frac{x^2}{9}-\frac{y^2}{16}=1$的渐近线方程为y=±$\frac{4}{3}$x;某抛物线的焦点与双曲线C的右焦点重合,则此抛物线的标准方程为y2=20x.分析 由条件利用双曲线、抛物线的简单性质,得出结论.
解答 解:双曲线$C:\frac{x^2}{9}-\frac{y^2}{16}=1$的渐近线方程为 y=±$\frac{4}{3}$x,
由于双曲线$C:\frac{x^2}{9}-\frac{y^2}{16}=1$的右焦点为(5,0),设此抛物线的标准方程为y2=2px,
则$\frac{p}{2}$=5,p=10,故抛物线的方程为y2=20x,
故答案为:$y=±\frac{4}{3}x;\;\;{y^2}=20x$.
点评 本题主要考查双曲线、抛物线的简单性质的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.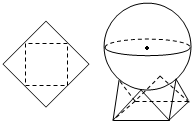 用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )
用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )
 用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )
用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )| A. | $\frac{\sqrt{2}+2}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | C. | $\frac{\sqrt{10}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{10}-\sqrt{2}}{2}$ |
11.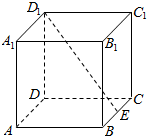 如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
 如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 3 |
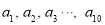 的平均数为
的平均数为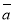 ,样本
,样本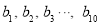 的平均数为
的平均数为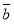 ,那么样本
,那么样本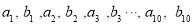 的平均数为( )
的平均数为( )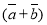 B.
B.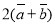 C.
C. 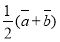 D.
D. 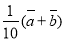
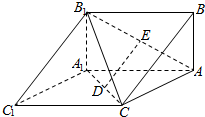 如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2$\sqrt{2}$,AA1=AC=4,∠A1C1C=60°,D、E分别为A1C,AB1的中点.
如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2$\sqrt{2}$,AA1=AC=4,∠A1C1C=60°,D、E分别为A1C,AB1的中点.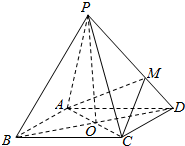 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BCD=120°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PC=2.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BCD=120°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PC=2.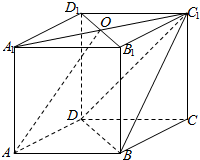 在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1与B1D1的交点,已知AA1=AB=1,∠BAD=60°.
在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1与B1D1的交点,已知AA1=AB=1,∠BAD=60°.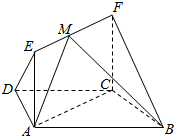 如图,矩形ACFE⊥底面ABCD,底面ABCD为等腰梯形,且AB∥CD,AB=2AD=2CD=2CF.
如图,矩形ACFE⊥底面ABCD,底面ABCD为等腰梯形,且AB∥CD,AB=2AD=2CD=2CF.