题目内容
6.已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若m,n∈[-1,1],m+n≠0 时,有$\frac{f(m)+f(n)}{m+n}>0$.(1)求证:f(x)在[-1,1]上为增函数;
(2)求不等式$f(x+\frac{1}{2})<f(1-x)$的解集;
(3)若$f(x)≤{t^2}+t-\frac{1}{{{{cos}^2}α}}-2tanα-1$对所有$x∈[-1,1],α∈[-\frac{π}{3},\frac{π}{4}]$恒成立,求实数t的取值范围.
分析 (1)由条件利用增函数的定义证得结论.
(2)根据函数的奇偶性和单调性,把要解的不等式等价转化为一个不等式组,求得此不等式的解集即可.
(3)根据函数的单调性求得f(x)的最大值,可得t2+t≥g(α)=$\frac{1}{{cos}^{2}α}$+2tanα+2 对$?α∈[-\frac{π}{3},\frac{π}{4}]$的恒成立,再求得g(α)的最大值,从而求得t的范围.
解答 解:(1)证明:任取x1,x2∈[-1,1]且x1<x2,则$f({x_2})-f({x_1})=f({x_2})+f(-{x_1})=\frac{{f({x_2})+f(-{x_1})}}{{{x_2}+(-{x_1})}}•({x_2}-{x_1})>0$,
∴f(x2)>f(x1),∴f(x)为增函数.
(2)$f(x+\frac{1}{2})<f(1-x)$,等价于$\left\{\begin{array}{l}{-1≤x+\frac{1}{2}≤1}\\{-1≤1-x≤1}\\{x+\frac{1}{2}<1-x}\end{array}\right.$,求得0≤x<$\frac{1}{4}$,
即不等式$f(x+\frac{1}{2})<f(1-x)$的解集为$[0,\frac{1}{4})$.
(3)由于f(x)为增函数,
∴f(x)的最大值为$f(1)=1≤{t^2}+t-\frac{1}{{{{cos}^2}α}}-2tanα-1$对$α∈[-\frac{π}{3},\frac{π}{4}]$恒成立$?{t^2}+t≥\frac{1}{{{{cos}^2}α}}+2tanα+2$ 对$?α∈[-\frac{π}{3},\frac{π}{4}]$的恒成立,
设$g(α)=\frac{1}{{{{cos}^2}α}}+2tanα+2$,则${t^2}+t≥{(g(α))_{max}},α∈[-\frac{π}{3},\frac{π}{4}]$.
又$g(α)=\frac{1}{{{{cos}^2}α}}+2tanα+2$=$\frac{{{{cos}^2}α+{{sin}^2}α}}{{{{cos}^2}α}}+2tanα+2$=1+tan2α+2tanα+2=(tanα+1)2+2,
∵α∈[-$\frac{π}{3}$,$\frac{π}{4}$],∴tanα∈[-$\sqrt{3}$,1],故当tanα=1时,
${(g(α))_{max}}=g(\frac{π}{4})=6$.
∴t2+t≥6,求得t≤-3 t≥2,即为所求的实数t的取值范围.
点评 本题主要考查函数的单调性的证明以及应用,函数的恒成立问题,求函数的最值,属于中档题.

| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充条件 | D. | 既非充分条件也非必要条件 |
| A. | (-$\frac{3}{5}$,-$\frac{4}{5}$) | B. | (-$\frac{4}{5}$,$\frac{3}{5}$) | C. | (-$\frac{3}{5}$,-$\frac{4}{5}$),($\frac{3}{5}$,$\frac{4}{5}$) | D. | ($±\frac{3}{5}$,$±\frac{4}{5}$) |
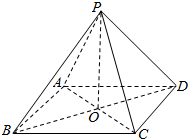 已知P是四边形ABCD所在平面外一点,PA=PB=PD,在四边形ABCD中,BA=AD,BA⊥AD,O是BD的中点,OC=$\frac{1}{2}$OA=$\frac{1}{3}$OP.
已知P是四边形ABCD所在平面外一点,PA=PB=PD,在四边形ABCD中,BA=AD,BA⊥AD,O是BD的中点,OC=$\frac{1}{2}$OA=$\frac{1}{3}$OP.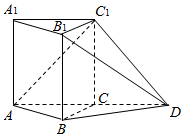 如图,在直棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=AA1=1,延长AC至D,使AC=CD,连接BD,B1D,C1D
如图,在直棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=AA1=1,延长AC至D,使AC=CD,连接BD,B1D,C1D 的夹角为60°,且
的夹角为60°,且 ,则
,则 ____________.
____________.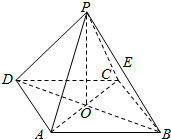 已知:正四棱锥P-ABCD,O为正方形ABCD的中心,PA与底ABCD所成的角为α,且cosα=$\frac{\sqrt{10}}{5}$.
已知:正四棱锥P-ABCD,O为正方形ABCD的中心,PA与底ABCD所成的角为α,且cosα=$\frac{\sqrt{10}}{5}$.