题目内容
5.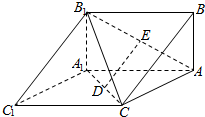 如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2$\sqrt{2}$,AA1=AC=4,∠A1C1C=60°,D、E分别为A1C,AB1的中点.
如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2$\sqrt{2}$,AA1=AC=4,∠A1C1C=60°,D、E分别为A1C,AB1的中点.(Ⅰ)求证:DE∥平面ABC;
(Ⅱ)求点B到平面AB1C的距离.
分析 (Ⅰ)推导出DE∥CB,由此能证明DE∥平面ABC.
(Ⅱ)取AA1的中点为F,连结CF,由${V}_{C-AB{B}_{1}}={V}_{B-A{B}_{1}C}$,能求出点B到平面AB1C的距离.
解答 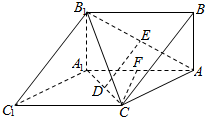 证明:(Ⅰ)E为AB1的中点,即E为AB1与A1B的交点,
证明:(Ⅰ)E为AB1的中点,即E为AB1与A1B的交点,
又D为A1C的中点,∴DE∥CB,
∵DE?平面ABC,CB?平面ABC,
∴DE∥平面ABC.
解:(Ⅱ)取AA1的中点为F,连结CF,
∵AA1=AC=4,∠A1C1C=60°,得△ACA1为正三角形,
∴CF⊥AA1,且CF=2$\sqrt{3}$,
∵BA⊥平面AA1C1C,∴BA⊥CF,
∴CF⊥平面ABB1A1,
在直角△B1A1C中,A1B1=2$\sqrt{2}$,A1C=4,则B1C=2$\sqrt{6}$,
在等腰△AB1C中,$A{B}_{1}={B}_{1}C=2\sqrt{6}$,AC=4,
∴${S}_{△A{B}_{1}C}$=4$\sqrt{5}$,
设点B到平面AB1C的距离为h,
∵${V}_{C-AB{B}_{1}}={V}_{B-A{B}_{1}C}$,
∴$\frac{1}{3}×\frac{1}{2}×AB×B{B}_{1}×CF=\frac{1}{3}×{S}_{△A{B}_{1}C}×h$,
解得h=$\frac{2\sqrt{30}}{5}$,
∴点B到平面AB1C的距离为$\frac{2\sqrt{30}}{5}$.
点评 本题考查线面平行的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意等体积法的合理运用.

练习册系列答案
相关题目
13.已知边长为3的正三角形ABC的三个顶点都在半径为2的球O的球面上,则点O到平面ABC的距离为( )
| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
14.函数f(x)在x=x0处导数存在,若p:f′(x0)=0;q:x=x0是f(x)的极值点,则p是q的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充条件 | D. | 既非充分条件也非必要条件 |
 =(-8,1),
=(-8,1), =(3,4),则
=(3,4),则 方向上的射影是
方向上的射影是 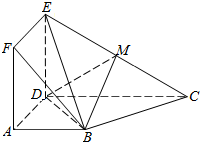 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,点M是线段EC的中点.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,点M是线段EC的中点.
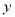 (单位:元)关于当天需求量
(单位:元)关于当天需求量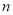 (单位:个,
(单位:个,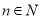 )的函数解析式;
)的函数解析式;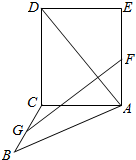 如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点,求
如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点,求 如图,已知斜三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧面BB1C1C是菱形,∠B1BC=60°.
如图,已知斜三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧面BB1C1C是菱形,∠B1BC=60°.