题目内容
5.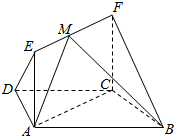 如图,矩形ACFE⊥底面ABCD,底面ABCD为等腰梯形,且AB∥CD,AB=2AD=2CD=2CF.
如图,矩形ACFE⊥底面ABCD,底面ABCD为等腰梯形,且AB∥CD,AB=2AD=2CD=2CF.(1)求证:BC⊥平面ACFE;
(2)当点M在线段EF上运动时,求平面MAB与平面FCB所成锐二面角余弦的取值范围.
分析 (1)由面面垂直得CF⊥BC,由余弦定理得AC⊥BC,由此能证明BC⊥平面ACFE.
(2)建立分别以直线CA、CB、CF为x轴,y轴,z轴的空间直角坐标系,利用向量法能求出平面MAB与平面FCB所成锐二面角余弦的取值范围.
解答  证明:(1)平面ACFE⊥平面ABCD且平面ACFE∩平面ABCD=AC,
证明:(1)平面ACFE⊥平面ABCD且平面ACFE∩平面ABCD=AC,
又∵矩形ACFE中,CF⊥AC∴CF⊥平面ABCD,
∴CF⊥BC,
∵底面ABCD为等腰梯形,且AB∥CD,AB=2AD=2CD=2CF,设AB=2,∠ABC=θ,
∴AC2=AD2+CD2+2•AD•CD•cosθ=AB2+BC2-2•AB•BC•cosθ,
∴1+1+2cosθ=4+1-4cosθ,解得cosθ=$\frac{1}{2}$,∴θ=60°.
∴AC=$\sqrt{1+1+2×\frac{1}{2}}$=$\sqrt{3}$,∴AC2+BC2=AB2,∴AC⊥BC,
又AC∩FC=C,∴BC⊥平面ACFE.
解:(2)由(1)可建立分别以直线CA、CB、CF为x轴,y轴,z轴的如图所示空间直角坐标系,
令EM=λ(0$≤λ≤\sqrt{3}$),则C(0,0,0),A($\sqrt{3}$,0,0),B(0,1,0),M(λ,0,1),
∴$\overrightarrow{AB}$=(-$\sqrt{3}$,1,0),$\overrightarrow{BM}$=(λ,-1,1).
设$\overrightarrow{{n}_{1}}$=(x,y,z)为平面MAB的一个法向量,
由$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{AB}=-\sqrt{3}x+y=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{BM}=λx-y+z=0}\end{array}\right.$,取x=1,则$\overrightarrow{{n}_{1}}=(1,\sqrt{3},\sqrt{3}-λ)$,
∵$\overrightarrow{{n}_{2}}$=(1,0,0)是平面FCB的一个法向量,
∴cosθ=$\frac{|\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}|}{|\overrightarrow{{n}_{1}}|•|\overrightarrow{{n}_{2}}|}$=$\frac{1}{\sqrt{1+3+(\sqrt{3}-λ)^{2}}×1}$=$\frac{1}{\sqrt{(λ-\sqrt{3})^{2}}+4}$,
∵0$≤λ≤\sqrt{3}$,∴当λ=0时,cosθ有最小值$\frac{\sqrt{7}}{7}$,
当$λ=\sqrt{3}$时,cosθ有最大值$\frac{1}{2}$,∴cosθ∈[$\frac{\sqrt{7}}{7}$,$\frac{1}{2}$].
∴平面MAB与平面FCB所成锐二面角余弦的取值范围是[$\frac{\sqrt{7}}{7}$,$\frac{1}{2}$].
点评 本题考查线面垂直的证明,考查面面角的余弦值的取值范围的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充条件 | D. | 既非充分条件也非必要条件 |
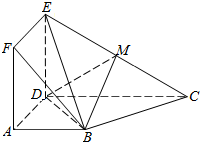 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,点M是线段EC的中点.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,点M是线段EC的中点.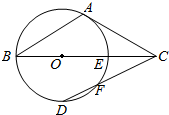 如图,C点在圆O直径BE的延长线上,CA切圆O于A点,CE=OE,CD交⊙O于点D、F.
如图,C点在圆O直径BE的延长线上,CA切圆O于A点,CE=OE,CD交⊙O于点D、F.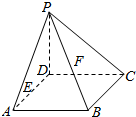 已知在四棱锥P-ABCD中,底面ABCD为菱形且∠ADC=120°,E,F分别是AD,PB的中点且PD=AD
已知在四棱锥P-ABCD中,底面ABCD为菱形且∠ADC=120°,E,F分别是AD,PB的中点且PD=AD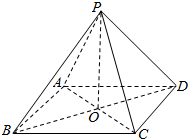 已知P是四边形ABCD所在平面外一点,PA=PB=PD,在四边形ABCD中,BA=AD,BA⊥AD,O是BD的中点,OC=$\frac{1}{2}$OA=$\frac{1}{3}$OP.
已知P是四边形ABCD所在平面外一点,PA=PB=PD,在四边形ABCD中,BA=AD,BA⊥AD,O是BD的中点,OC=$\frac{1}{2}$OA=$\frac{1}{3}$OP.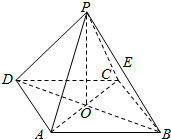 已知:正四棱锥P-ABCD,O为正方形ABCD的中心,PA与底ABCD所成的角为α,且cosα=$\frac{\sqrt{10}}{5}$.
已知:正四棱锥P-ABCD,O为正方形ABCD的中心,PA与底ABCD所成的角为α,且cosα=$\frac{\sqrt{10}}{5}$.