题目内容
11.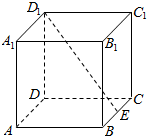 如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 3 |
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出线段B1P的长度的最大值.
解答  解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设P(a,b,0),则D1(0,0,2),E(1,2,0),B1(2,2,2),
$\overrightarrow{{B}_{1}P}$=(a-2,b-2,-2),$\overrightarrow{{D}_{1}E}$=(1,2,-2),
∵B1P⊥D1E,∴$\overrightarrow{{B}_{1}P}•\overrightarrow{{D}_{1}E}$=a-2+2(b-2)+4=0,
∴a+2b-2=0,
∴点P的轨迹是一条线段,当a=0时,b=1;当b=0时,a=2,
设CD中点F,则点P在线段AF上,
当A与P重合时,线段B1P的长度为:|AB1|=$\sqrt{4+4}$=2$\sqrt{2}$;
当P与F重合时,P(0,1,0),$\overrightarrow{{B}_{1}P}$=(-2,-1,-2),线段B1P的长度|$\overrightarrow{{B}_{1}P}$|=$\sqrt{4+4+1}$=3,
当P在线段AF的中点时,P(1,$\frac{1}{2}$,0),$\overrightarrow{{B}_{1}P}$=(-1,-$\frac{3}{2}$,-2),线段B1P的长度|$\overrightarrow{{B}_{1}P}$|=$\sqrt{1+\frac{9}{4}+4}$=$\frac{\sqrt{29}}{2}$.
∴线段B1P的长度的最大值为3.
故选:D.
点评 本题考查线段长的最大值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{6}$ | C. | 6 | D. | 8 |
 的定义域是( )
的定义域是( )
 B.
B. C.
C. D.
D.
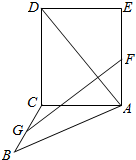 如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点,求
如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点,求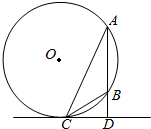 如图,A、B是圆O上的两点,且AB的长度小于圆O的直径,直线l与AB垂于点D且与圆O相切于点C.若AB=2,DB=1
如图,A、B是圆O上的两点,且AB的长度小于圆O的直径,直线l与AB垂于点D且与圆O相切于点C.若AB=2,DB=1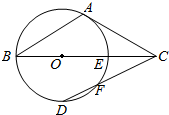 如图,C点在圆O直径BE的延长线上,CA切圆O于A点,CE=OE,CD交⊙O于点D、F.
如图,C点在圆O直径BE的延长线上,CA切圆O于A点,CE=OE,CD交⊙O于点D、F.