题目内容
1.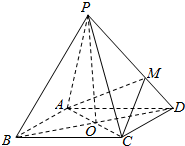 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BCD=120°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PC=2.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BCD=120°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PC=2.(1)若在棱PD上存在一点N,且BN∥面AMC,确定点N的位置,并说明理由;
(2)求三棱锥A-PMC的体积.
分析 (1)连结OM,BN,根据线面平行的性质得出BN∥OM,故$\frac{DO}{DB}=\frac{DM}{DN}$=$\frac{1}{2}$,所以N为PD的另一个三等分点;
(2)由菱形的性质可得OC=$\frac{1}{2}$AC=1,由勾股定理求出PO,于是V棱锥A-PMC=V棱锥P-ACD-V棱锥M-ACD=$\frac{2}{3}$V棱锥P-ACD.
解答 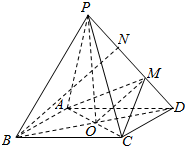 解:(1)连结OM,BN,
解:(1)连结OM,BN,
∵BN∥面AMC,BN?平面BDN,平面BDN∩平面ACM=OM,
∴BN∥OM,
∴$\frac{DO}{DB}=\frac{DM}{DN}$=$\frac{1}{2}$,
∵M是PD靠近D的三等分点,∴N是PD靠近P点的三等分点.
(2)∵底面ABCD是边长为2的菱形,∠BCD=120°,
∴AO=OC=1,△ACD是等边三角形.∴S△ACD=$\frac{\sqrt{3}}{4}A{C}^{2}$=$\sqrt{3}$.
∵PO⊥面ABCD,AC?平面ABCD,
∴PO⊥AC,∴PO=$\sqrt{P{C}^{2}-O{C}^{2}}$=$\sqrt{3}$,
∵M是靠近D点的三等分点,∴M到平面ABCD的距离h=$\frac{1}{3}$PO=$\frac{\sqrt{3}}{3}$.
∴V棱锥A-PMC=V棱锥P-ACD-V棱锥M-ACD=$\frac{1}{3}$S△ACD•PO-$\frac{1}{3}$S△ACD•$\frac{1}{3}$PO=$\frac{2\sqrt{3}}{9}$.
点评 本题考查了线面平行的性质,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
6.过点(2,-2)且以$y=±\frac{{\sqrt{2}}}{2}x$为渐近线的双曲线方程是( )
| A. | $\frac{y^2}{2}-\frac{x^2}{4}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{2}=1$ | C. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ | D. | $\frac{x^2}{2}-\frac{y^2}{4}=1$ |
13.已知边长为3的正三角形ABC的三个顶点都在半径为2的球O的球面上,则点O到平面ABC的距离为( )
| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
 ,则cos(α+
,则cos(α+ )=( )
)=( ) B.
B. C.
C. D.
D.
 (单位:元)关于当天需求量
(单位:元)关于当天需求量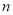 (单位:个,
(单位:个,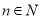 )的函数解析式;
)的函数解析式; 如图,已知斜三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧面BB1C1C是菱形,∠B1BC=60°.
如图,已知斜三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧面BB1C1C是菱形,∠B1BC=60°. 已知在四棱锥P-ABCD中,底面ABCD为菱形且∠ADC=120°,E,F分别是AD,PB的中点且PD=AD
已知在四棱锥P-ABCD中,底面ABCD为菱形且∠ADC=120°,E,F分别是AD,PB的中点且PD=AD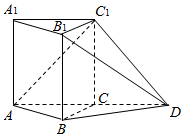 如图,在直棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=AA1=1,延长AC至D,使AC=CD,连接BD,B1D,C1D
如图,在直棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=AA1=1,延长AC至D,使AC=CD,连接BD,B1D,C1D