题目内容
10.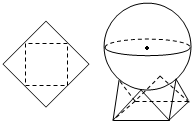 用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )
用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )| A. | $\frac{\sqrt{2}+2}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | C. | $\frac{\sqrt{10}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{10}-\sqrt{2}}{2}$ |
分析 蛋槽的边长是原来硬纸板的对角线长度的一半,为$\sqrt{2}$cm,蛋槽立起来的小三角形部分高度是$\frac{\sqrt{2}}{2}$cm,由此能求出球体球心与蛋巢底面的距离.
解答 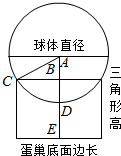 解:蛋槽的边长是原来硬纸板的对角线长度的一半,为$\sqrt{2}$cm,
解:蛋槽的边长是原来硬纸板的对角线长度的一半,为$\sqrt{2}$cm,
蛋槽立起来的小三角形部分高度是$\frac{\sqrt{2}}{2}$,
半径为$\sqrt{2}$的球体放置于蛋巢上,得到r=$\sqrt{2}$cm,
直径D=2$\sqrt{2}$cm,大于折好的蛋巢边长$\sqrt{2}$cm,
四个三角形的顶点所在的平面在鸡蛋表面所截取的小圆直径就是蛋槽的边长$\sqrt{2}$cm,
根据图示,AB段由三角形AB求出得:AB=$\sqrt{(\sqrt{2})^{2}-(\frac{\sqrt{2}}{2})^{2}}$=$\frac{\sqrt{6}}{2}$,
AE=AB+BE=$\frac{\sqrt{6}}{2}$+$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$,
∴球体球心与蛋巢底面的距离为$\frac{\sqrt{6}+\sqrt{2}}{2}$.
故选:B.
点评 本题考查点、线、面间距离的计算,解题时要认真审题,注意挖掘题设中的隐含条件,合理地化空间问题为平面问题,注意数形结合法的合理运用.

练习册系列答案
相关题目
14.tan23°+tan97°-$\sqrt{3}$tan23°tan97°=( )
| A. | -2 | B. | -2$\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 0 |
6.已知双曲线$\frac{x^2}{4}$-$\frac{y^2}{b^2}$=1(b>0)的离心率等于$\frac{\sqrt{3}}{3}$b,则该双曲线的焦距为( )
| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{6}$ | C. | 6 | D. | 8 |
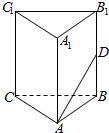 如图所示,在正三棱柱ABC-A1B1C1中,已知AB=1,D是棱BB1上的点,且BD=1,求:
如图所示,在正三棱柱ABC-A1B1C1中,已知AB=1,D是棱BB1上的点,且BD=1,求: 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,点M是线段EC的中点.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,点M是线段EC的中点.
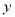 (单位:元)关于当天需求量
(单位:元)关于当天需求量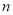 (单位:个,
(单位:个,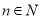 )的函数解析式;
)的函数解析式;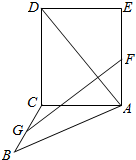 如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点,求
如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点,求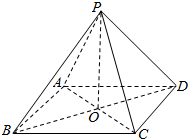 已知P是四边形ABCD所在平面外一点,PA=PB=PD,在四边形ABCD中,BA=AD,BA⊥AD,O是BD的中点,OC=$\frac{1}{2}$OA=$\frac{1}{3}$OP.
已知P是四边形ABCD所在平面外一点,PA=PB=PD,在四边形ABCD中,BA=AD,BA⊥AD,O是BD的中点,OC=$\frac{1}{2}$OA=$\frac{1}{3}$OP.