题目内容
13.已知△ABC中,A,B,C所对的边分别为a,b,c,且a>c>b,且a,c,b成等差数列,|AB|=2,求点C的轨迹方程.分析 运用等差数列的性质,再由椭圆的定义,即可得到轨迹方程,注意x<0.
解答 解:由于a>c,a,c,b成等差数列,c=|AB|=2,
则a+b=2c=4>|AB|=2,且a>c>b,
可设A,B在x轴上,由椭圆的定义,
可知顶点C的轨迹为椭圆的位于y轴左边的部分.
其长轴长为4,焦距为2,则短轴长为2$\sqrt{3}$.
则有顶点C的轨迹方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1(x<0).
点评 本题考查运用椭圆的定义球轨迹方程,考查等差数列的性质,考查运算能力,属于基础题和易错题.

练习册系列答案
相关题目
3.在△ABC中,已知$cosA=\frac{1}{2}$,则sinA=( )
| A. | $\frac{1}{2}$ | B. | ±$\frac{\sqrt{3}}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
8.方程y=$\sqrt{36-{x}^{2}}$表示的曲线是( )
| A. | 一个圆 | B. | 两条射线 | C. | 半个圆 | D. | 一条射线 |
5.若5555=8k+r(k,r为自然数),则r的最小值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
1.已知α是三角形的内角,且$cosα=-\frac{3}{5}$,则tanα等于( )
| A. | $-\frac{4}{3}$ | B. | $-\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
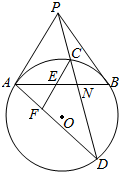 过圆外一点P向圆O作切线PA、PB及及割线PCD,过C作PA的平行线,分别交AB、AD与于E、F.求证:CE=EF.
过圆外一点P向圆O作切线PA、PB及及割线PCD,过C作PA的平行线,分别交AB、AD与于E、F.求证:CE=EF.