题目内容
5.若5555=8k+r(k,r为自然数),则r的最小值为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 利用二项式定理化简求解即可.
解答 解:5555=(56-1)55=8k+r,而(56-1)55的展开式共有56项,除去最后一项,其余都被8整除,最后一项是-1,
所以写成8k+r,(k,r为自然数)则整数r可以为:7.
故选:D.
点评 本题考查二项式定理的应用,考查整除的性质,基本知识的考查.

练习册系列答案
相关题目
16.已知F1,F2分别是双曲线x2-$\frac{{y}^{2}}{24}$的=1左、右焦点,P是双曲线上的一点,若|PF1|,|PF2|,|F1F2|构成公差为正数的等差数列,则△F1PF2的面积为( )
| A. | 24 | B. | 22 | C. | 18 | D. | 12 |
10.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-2x,x≤0}\\{{e}^{x}-1,x>0}\end{array}\right.$,若f(x)≥ax,则a的取值范围是( )
| A. | (-∞,0] | B. | (-∞,1] | C. | [-2,0] | D. | [-2,1] |
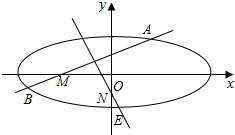 已知过点M(-1,0)的直线交椭圆:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,且当直线AB垂直x轴时,|AB|=$\sqrt{3}$.
已知过点M(-1,0)的直线交椭圆:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,且当直线AB垂直x轴时,|AB|=$\sqrt{3}$.