题目内容
4.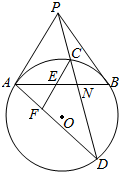 过圆外一点P向圆O作切线PA、PB及及割线PCD,过C作PA的平行线,分别交AB、AD与于E、F.求证:CE=EF.
过圆外一点P向圆O作切线PA、PB及及割线PCD,过C作PA的平行线,分别交AB、AD与于E、F.求证:CE=EF.
分析 由已知得P、C、N、D为调和点列,设FC交AP于无穷远点M,F、E、C、M为调和点列,由此能证明CE=EF.
解答  解:设PD交AB为N,
解:设PD交AB为N,
∵过圆外一点P向圆O作切线PA、PB及及割线PCD,过C作PA的平行线,分别交AB、AD与于E、F,
∴AB为极线,P、C、N、D为调和点列,
AD、AN、AC、AP为调和线束,
∵FC∥AP,
设FC交AP于无穷远点M,
则F、E、C、M为调和点列,
∴$\frac{EF}{CE}=\frac{FM}{CM}$=1,
∴CE=EF.
点评 本题考查两线段相等的证明,是中档题,解题时要认真审题,注意圆的简单性质和调和点列及调和光束的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14. 在班级的演讲比赛中,将甲、乙两名同学的得分情况制成如图所示的茎叶图.记甲、乙两名同学所得分数的平均分分别为$\overline x$甲、$\overline x$乙,则下列判断正确的是( )
在班级的演讲比赛中,将甲、乙两名同学的得分情况制成如图所示的茎叶图.记甲、乙两名同学所得分数的平均分分别为$\overline x$甲、$\overline x$乙,则下列判断正确的是( )
 在班级的演讲比赛中,将甲、乙两名同学的得分情况制成如图所示的茎叶图.记甲、乙两名同学所得分数的平均分分别为$\overline x$甲、$\overline x$乙,则下列判断正确的是( )
在班级的演讲比赛中,将甲、乙两名同学的得分情况制成如图所示的茎叶图.记甲、乙两名同学所得分数的平均分分别为$\overline x$甲、$\overline x$乙,则下列判断正确的是( )| A. | $\overline x$甲<$\overline x$乙,甲比乙成绩稳定 | B. | $\overline x$甲>$\overline x$乙,甲比乙成绩稳定 | ||
| C. | $\overline x$甲<$\overline x$乙,乙比甲成绩稳定 | D. | $\overline x$甲>$\overline x$乙,乙比甲成绩稳定 |
9.根据统计某种改良土豆亩产增加量y(百斤)与每亩使用农夫1号肥料x(千克)之间有如下的对应数据:
(1)画出数据的散点图.
(2)依据表中数据,请用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;并根据所求线性回归方程,估计如果每亩使用农夫1号肥料10千克,则这种改良土豆亩产增加量y是多少斤?
参考公式:
1.回归方程系数公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$
2.$\sum_{i=1}^{5}$xi2=145,$\sum_{i=1}^{5}$xiyi=106.
| x(千克) | 2 | 4 | 5 | 6 | 8 |
| y(百斤) | 3 | 4 | 4 | 4 | 5 |
(2)依据表中数据,请用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;并根据所求线性回归方程,估计如果每亩使用农夫1号肥料10千克,则这种改良土豆亩产增加量y是多少斤?
参考公式:
1.回归方程系数公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$
2.$\sum_{i=1}^{5}$xi2=145,$\sum_{i=1}^{5}$xiyi=106.
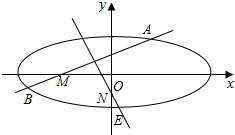 已知过点M(-1,0)的直线交椭圆:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,且当直线AB垂直x轴时,|AB|=$\sqrt{3}$.
已知过点M(-1,0)的直线交椭圆:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)于A,B两点,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,且当直线AB垂直x轴时,|AB|=$\sqrt{3}$.