题目内容
5.将函数y=sin(x+$\frac{π}{4}$)图象上的所有点纵坐标不变,横坐标变为原来的$\frac{1}{2}$倍,所得函数为f(x),则函数f(x)=$f(x)=sin(2x+\frac{π}{4})$.分析 根据函数y=Asin(ωx+φ)的图象变换规律可得答案.
解答 解:函数y=sin(x+$\frac{π}{4}$)图象上的所有点纵坐标不变,横坐标变为原来的$\frac{1}{2}$倍,周期变小,可得sin($\frac{1}{2}$x+$\frac{π}{4}$),即函数为f(x)=sin($\frac{1}{2}$x+$\frac{π}{4}$),
故答案为:$f(x)=sin(2x+\frac{π}{4})$.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
16.在等比数列{an}中,a1=-16,a4=$\frac{1}{4}$则q=( )
| A. | q=$\frac{1}{4}$ | B. | q=-$\frac{1}{4}$ | C. | q=4 | D. | q=-4 |
17.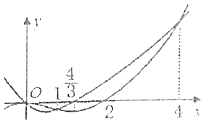 已知函数f(x)与f'(x)的图象如图所示,则函数$g(x)=\frac{f(x)}{e^x}$的单调递增区间为( )
已知函数f(x)与f'(x)的图象如图所示,则函数$g(x)=\frac{f(x)}{e^x}$的单调递增区间为( )
 已知函数f(x)与f'(x)的图象如图所示,则函数$g(x)=\frac{f(x)}{e^x}$的单调递增区间为( )
已知函数f(x)与f'(x)的图象如图所示,则函数$g(x)=\frac{f(x)}{e^x}$的单调递增区间为( )| A. | (0,4) | B. | $({-∞,1}),({\frac{4}{3},4})$ | C. | (0,1),(4,+∞) | D. | (-∞,0),(1,4) |
15.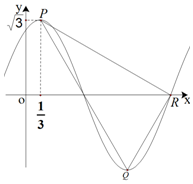 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )| A. | $f(x)=\sqrt{3}sin(\frac{π}{2}x+\frac{π}{3})$ | B. | $f(x)=\sqrt{3}sin(\frac{π}{2}x-\frac{π}{6})$ | ||
| C. | $f(x)=\sqrt{3}sin(\frac{2π}{3}x+\frac{5π}{18})$ | D. | $f(x)=\sqrt{3}sin(πx+\frac{π}{6})$ |