题目内容
6.实数x,y满足$\left\{\begin{array}{l}{x≤1}\\{y≤2}\\{2x+y-2≥0}\end{array}\right.$,则x2+y2的最大值是4;最小值是$\frac{4}{5}$.分析 先根据条件画出可行域,z=x2+y2,再利用几何意义求最值,只需求出可行域内的点到原点距离的最值,从而得到z最值即可.
解答  解:先根据约束条件画出可行域:
解:先根据约束条件画出可行域:
而z=x2+y2,
表示可行域内点到原点距离的平方,
点在阴影区域里运动时,点P到点O,OP最大
当在点P(1,2),z最大,最大值为02+22=4,
Q在直线2x+y-2=0,OQ与直线垂直距离最小,
可得z的最小值为:$(\frac{|-2|}{\sqrt{{2}^{2}+{1}^{2}}})^{2}$=$\frac{4}{5}$,
故答案为:4;$\frac{4}{5}$.
点评 本题主要考查了简单的线性规划,以及利用几何意义求最值,解决时,首先要解决的问题是明白题目中目标函数的意义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.在等比数列{an}中,a1=-16,a4=$\frac{1}{4}$则q=( )
| A. | q=$\frac{1}{4}$ | B. | q=-$\frac{1}{4}$ | C. | q=4 | D. | q=-4 |
17.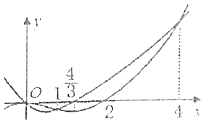 已知函数f(x)与f'(x)的图象如图所示,则函数$g(x)=\frac{f(x)}{e^x}$的单调递增区间为( )
已知函数f(x)与f'(x)的图象如图所示,则函数$g(x)=\frac{f(x)}{e^x}$的单调递增区间为( )
 已知函数f(x)与f'(x)的图象如图所示,则函数$g(x)=\frac{f(x)}{e^x}$的单调递增区间为( )
已知函数f(x)与f'(x)的图象如图所示,则函数$g(x)=\frac{f(x)}{e^x}$的单调递增区间为( )| A. | (0,4) | B. | $({-∞,1}),({\frac{4}{3},4})$ | C. | (0,1),(4,+∞) | D. | (-∞,0),(1,4) |
1.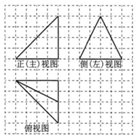 在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )
在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )
 在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )
在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )| A. | 4$\sqrt{3}$ | B. | 6 | C. | 4$\sqrt{2}$ | D. | 2$\sqrt{5}$ |
18.已知向量|$\overrightarrow{AB}$|=2,|$\overrightarrow{CD}$|=1,且|$\overrightarrow{AB}$-2$\overrightarrow{CD}$|=2$\sqrt{3}$,则向量$\overrightarrow{AB}$和$\overrightarrow{CD}$的夹角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
15.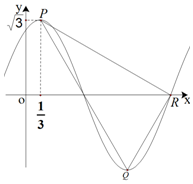 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )| A. | $f(x)=\sqrt{3}sin(\frac{π}{2}x+\frac{π}{3})$ | B. | $f(x)=\sqrt{3}sin(\frac{π}{2}x-\frac{π}{6})$ | ||
| C. | $f(x)=\sqrt{3}sin(\frac{2π}{3}x+\frac{5π}{18})$ | D. | $f(x)=\sqrt{3}sin(πx+\frac{π}{6})$ |
16.若点P是以F1,F2为焦点的双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)上一点,PF1⊥PF2,且|PF1|=2|PF2|,则此双曲线的标准方程是( )
| A. | x2-$\frac{{y}^{2}}{4}$=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | x2-$\frac{{y}^{2}}{5}$=1 | D. | x2-$\frac{{y}^{2}}{6}$=1 |
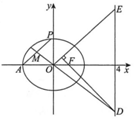 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为为$\frac{1}{2}$,F为椭圆C的右焦点A(-a,0),|AF|=3.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为为$\frac{1}{2}$,F为椭圆C的右焦点A(-a,0),|AF|=3.