题目内容
函数f(x)=2x-x2(0≤x≤3)的值域是 .
考点:二次函数在闭区间上的最值,函数的值域
专题:函数的性质及应用
分析:通过对二次函数f(x)配方即可得到该函数的最大值,最小值,从而求出f(x)的值域.
解答:
解:f(x)=-(x-1)2+1;
∴f(x)的最大值为1,最小值为f(3)=-3;
∴f(x)的值域是[-3,1].
故答案为:[-3,1].
∴f(x)的最大值为1,最小值为f(3)=-3;
∴f(x)的值域是[-3,1].
故答案为:[-3,1].
点评:考查通过对二次函数配方求二次函数的最值,从而求出该函数在闭区间上的值域的方法,以及函数值域的概念.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
已知
,且z=2x+y的最大值是最小值的3倍,则a的值是( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知点A(-1,0),B(1,0),P是平面内一动点,直线PA,PB斜率之积为-
,则动点P的轨迹方程为( )
| 1 |
| 2 |
| A、2x2+y2=1(x≠±1) |
| B、x2+2y2=1(x≠±1) |
| C、x2-2y2=1(x≠±1) |
| D、2x2-y2=1(x≠±1) |
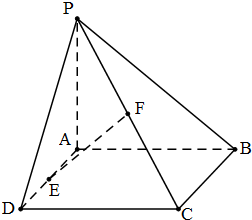 在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为矩形,PA=AB,E、F分别为AD、PC的中点,
在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为矩形,PA=AB,E、F分别为AD、PC的中点,