题目内容
已知S是△ABC所在平面外一点,∠ASC=90°,∠ASB=∠BSC=60°,且SA=SB=SC.
(1)求证:平面SAC⊥平面ABC;
(2)求二面角B-AS-C的余弦值.
(1)求证:平面SAC⊥平面ABC;
(2)求二面角B-AS-C的余弦值.
考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:对第(1)问,取AC的中点O,连结BO,SO,则∠BOS为二面角B-AC-S的平面角,只需计算出S0,BO,由勾股定理的逆定理可判断∠BOS=90°,即可得证.
对第(2)问,取AS的中点M,连结MO,MB,先证明∠BMO为二面角B-AS-C的平面角,再解△BMO即可.
对第(2)问,取AS的中点M,连结MO,MB,先证明∠BMO为二面角B-AS-C的平面角,再解△BMO即可.
解答:
解:(1)证明:取AC的中点O,连结BO,SO,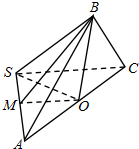 设SA=SB=SC=1,
设SA=SB=SC=1,
由条件易知,SO⊥AC,AC=
,SO=
AC=
,AB=BC=SA=1.
由AB2+BC2=AC2知,AB⊥BC,
∴BO⊥AC,且BO=
AC=
,∴SO2+BO2=SB2,
∴二面角B-AC-S的平面角∠BOS=90°,即平面SAC⊥平面ABC.
(2)取AS的中点M,连结MO,MB,由(1)知,△SAB与△SBC为全等的正三角形,
∴SA⊥MB,SA⊥MO,故∠BMO为二面角B-AS-C的平面角.
又由BO⊥AC及BO⊥SO,得BO⊥平面SAC,
在△BMO中,易得MO=
,MB=
,∴cos∠BMO=
=
.
 设SA=SB=SC=1,
设SA=SB=SC=1,由条件易知,SO⊥AC,AC=
| 2 |
| 1 |
| 2 |
| ||
| 2 |
由AB2+BC2=AC2知,AB⊥BC,
∴BO⊥AC,且BO=
| 1 |
| 2 |
| ||
| 2 |
∴二面角B-AC-S的平面角∠BOS=90°,即平面SAC⊥平面ABC.
(2)取AS的中点M,连结MO,MB,由(1)知,△SAB与△SBC为全等的正三角形,
∴SA⊥MB,SA⊥MO,故∠BMO为二面角B-AS-C的平面角.
又由BO⊥AC及BO⊥SO,得BO⊥平面SAC,
在△BMO中,易得MO=
| ||
| 2 |
| ||
| 2 |
| MO |
| MB |
| ||
| 3 |
点评:本题考查了面面垂直的判定方法及二面角大小的求法,本题使用的均为定义法,其一般步骤分别为:
1.利用定义法证明面面垂直:第一步,作出二面角的平面角;第二步,证明此平面角为90°,即可下结论.
2.利用定义法求二面角的大小:
第一步,作出二面角的平面角,即在二面角的棱上取一点,过该点分别在两个半平面内作棱的垂射线;
第二步,将此平面角放在一个三角形中,解此三角形即可.
1.利用定义法证明面面垂直:第一步,作出二面角的平面角;第二步,证明此平面角为90°,即可下结论.
2.利用定义法求二面角的大小:
第一步,作出二面角的平面角,即在二面角的棱上取一点,过该点分别在两个半平面内作棱的垂射线;
第二步,将此平面角放在一个三角形中,解此三角形即可.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
已知函数f(x)=
sin2x+cos2x-m在[0,
]上有两个零点,则实数m的取值范围是( )
| 3 |
| π |
| 2 |
| A、(-1,2) |
| B、[1,2) |
| C、(-1,2] |
| D、[1,2] |
已知函数f(x)=
,若f(a)-f(-a)≤2f(1),则a的取值范围是( )
|
| A、[1,+∞) |
| B、(-∞,1] |
| C、[-1,1] |
| D、[-2,2] |
已知a,b,c是实数,下列命题是真命题的有( )个
①“a>b”是“a2>b2”的充分条件;
②“a>b”是“a2>b2”的必要条件;
③“a>b”是“ac2>bc2”的充分条件;
④“a>b”是“|a|>|b|”的充要条件.
①“a>b”是“a2>b2”的充分条件;
②“a>b”是“a2>b2”的必要条件;
③“a>b”是“ac2>bc2”的充分条件;
④“a>b”是“|a|>|b|”的充要条件.
| A、0 | B、1 | C、2 | D、3 |
若实数x,y满足不等式组
,则目标函数z=x-2y的最大值是( )
|
| A、1 | B、2 | C、3 | D、4 |