题目内容
3.已知e是自然对数的底数,实数a,b满足eb=2a-3,则|2a-b-1|的最小值为3.分析 利用已知条件化简表达式,利用构造法以及函数的导数求解函数的最值.
解答 解:e是自然对数的底数,实数a,b满足eb=2a-3,2a-3>0,可得b=ln(2a-3),
|2a-b-1|=|2a-ln(2a-3)-1|,令2a-3=x,上式化为|x-lnx+2|,
令y=x-lnx+2,可得y′=1-$\frac{1}{x}$,由y′=0,可得x=1,当x∈(0,1)时,y′<0,函数是减函数,
x>1时,y′>0,函数是增函数,x=1时,y=x-lnx取得最小值:3.
则|2a-b-1|的最小值为3.
故答案为:3.
点评 本题考查函数的最值的求法,导数的综合应用,考查构造法以及分析问题解决问题的能力.

练习册系列答案
相关题目
15.已知复数z=$\frac{2-3i}{1+i}$(i为虚数单位),则z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.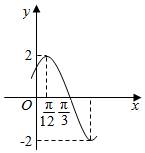 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )| A. | ω=2,φ=$\frac{π}{6}$ | |
| B. | f(x)的图象关于点(-$\frac{5π}{12}$,0)对称 | |
| C. | 若方程f(x)=m在[-$\frac{π}{2}$,0]上有两个不相等的实数根,则实数m的取值范围是(-2,-$\sqrt{3}$] | |
| D. | 将函数y=2cos(2x+$\frac{π}{3}$)的图象向右平移$\frac{π}{12}$的单位得到函数f(x)的图象 |
13.函数y=cos2x+cos2x的最大值是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
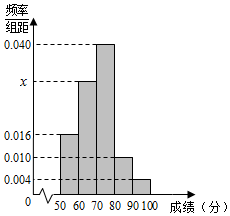 某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100]的有2人,由此推测频率分布直方图中的x=0.03.
某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100]的有2人,由此推测频率分布直方图中的x=0.03.