题目内容
13.函数y=cos2x+cos2x的最大值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
分析 由三角函数公式化简可得y=3cos2x-1,由三角函数的知识可得函数取最大值2
解答 解:由三角函数公式化简可得y=cos2x+cos2x
=cos2x+2cos2x-1=3cos2x-1,
∴当cosx=±1时,函数取最大值2,
故选:A.
点评 本题考查三角函数的最值,涉及二倍角公式,属基础题.

练习册系列答案
相关题目
5.已知M为不等式组$\left\{\begin{array}{l}{y{≤x}^{2}}\\{1≤x≤2}\\{y≥0}\end{array}\right.$,表示的平面区域,直线l:y=2x+a,当a从-2连续变化到0时.则区域M被直线l扫过的面积为( )
| A. | $\frac{7}{3}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{4}{3}$ |
 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为4,10,则输出的a为( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为4,10,则输出的a为( ) 设P是正六边形OABCDE的中心,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,试用向量$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{PB}$、$\overrightarrow{OC}$、$\overrightarrow{OD}$.
设P是正六边形OABCDE的中心,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,试用向量$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{PB}$、$\overrightarrow{OC}$、$\overrightarrow{OD}$.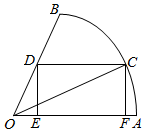 圆心角为60°的扇形AOB的半径为1,C是AB弧上一点,作矩形CDEF,如图,当C点在什么位置时,这个矩形的面积最大?这时的;∠AOC等于多少度?
圆心角为60°的扇形AOB的半径为1,C是AB弧上一点,作矩形CDEF,如图,当C点在什么位置时,这个矩形的面积最大?这时的;∠AOC等于多少度?