题目内容
13.已知△ABC的内角A,B,C的对边分别为a,b,c,$\overrightarrow{m}$=($\frac{a}{sin(A+B)}$,c-2b),$\overrightarrow{n}$=(sin2C,1),且满足$\overrightarrow{m}•\overrightarrow{n}$=0.(1)求∠A的大小;
(2)若a=1,求△ABC周长的取值范围.
分析 ( I)由已知及平面向量数量积的运算可得2acosC+c-2b=0,由余弦定理整理得b2+c2-a2=bc,可求cosA=$\frac{1}{2}$,结合范围0<A<π,即可解得A的值.
( II)由正弦定理及恒等变换的应用可得△ABC的周长l=a+b+c=1+$\frac{2\sqrt{3}}{3}$(sinB+sinC)=2sin(B+$\frac{π}{6}$)+1,结合范围0<B<$\frac{2π}{3}$,可求$\frac{1}{2}$<sin(B+$\frac{π}{6}$)≤1,即可得解周长的取值范围.
解答 (本小题满分12分)
解:( I)∵$\overrightarrow{m}•\overrightarrow{n}$=0,∴$\frac{a}{sin(A+B)}$•sin2C+c-2b=,…(2分)
∴$\frac{a}{sinC}•2sinCcosC+c-2b=0$,即2acosC+c-2b=0,…(3分)
由余弦定理得:2a•$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$+c-2b=0,…(4分)
整理得b2+c2-a2=bc,∴cosA=$\frac{1}{2}$,∵0<A<π,∴A=$\frac{π}{3}$.…(6分)
( II)∵cosA=$\frac{1}{2}$,∴sinA=$\frac{\sqrt{3}}{2}$,…(7分)
由正弦定理得:$\frac{b}{sinB}=\frac{c}{sinC}=\frac{a}{sinA}$=$\frac{1}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{3}}{3}$,…(8分)
△ABC的周长l=a+b+c=1+$\frac{2\sqrt{3}}{3}$(sinB+sinC)=1+$\frac{2\sqrt{3}}{3}$[sinB+sin(B+$\frac{π}{3}$)]
=2sin(B+$\frac{π}{6}$)+1,…(10分)
∵0<B<$\frac{2π}{3}$,∴$\frac{π}{6}$<B$+\frac{π}{6}$<$\frac{5π}{6}$,∴$\frac{1}{2}$<sin(B+$\frac{π}{6}$)≤1,…(11分)
因此2<l≤3,故△ABC周长的取值范围为(2,3].…(12分)
点评 本题主要考查了平面向量数量积的运算,正弦定理,余弦定理,正弦函数的图象和性质在解三角形中的综合应用,考查了转化思想和数形结合思想的应用,考查了计算能力,属于中档题.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案| A. | 2$\sqrt{2}$ | B. | 4 | C. | 8 | D. | 16 |
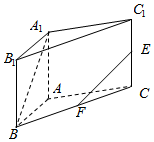 直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=2$\sqrt{2}$,E,F分别是CC1,BC的中点,求:
直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=2$\sqrt{2}$,E,F分别是CC1,BC的中点,求: