题目内容
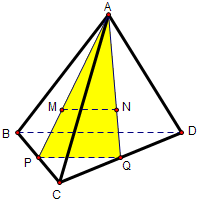
如图所示，A是△BCD所在平面外一点，M，N分别是△ABC和△ACD的重心，若∠BCD=90°，BC=10，CD=8，则MN=考点：棱锥的结构特征
专题：空间位置关系与距离
分析：由已知条件求出BD=2
，连结AM交延长交BC于P，连结AN延长，交CD于Q，则PQ为△BCD的中位线，MN=
PQ，由此能求出结果．
| 41 |
| 2 |
| 3 |
解答：
解：∵∠BCD=90°，BC=10，CD=8，
∴BD=
=2
，
连结AM交延长交BC于P，连结AN延长，交CD于Q，
∵M，N分别是△ABC和△ACD的重心，
∴PQ为△BCD的中位线，
∴PQ∥BD且PQ=
=
，
∵AM：AP=AN：AQ=2：3，
∴MN=
PQ=
．
故答案为：
．
解：∵∠BCD=90°，BC=10，CD=8，∴BD=
| 102+82 |
| 41 |
连结AM交延长交BC于P，连结AN延长，交CD于Q，
∵M，N分别是△ABC和△ACD的重心，
∴PQ为△BCD的中位线，
∴PQ∥BD且PQ=
| BD |
| 2 |
| 41 |
∵AM：AP=AN：AQ=2：3，
∴MN=
| 2 |
| 3 |
| 2 |
| 3 |
| 41 |
故答案为：
| 2 |
| 3 |
| 41 |
点评：本题考查线段长的求法，是基础题，解题时要注意勾股定理、重心性质的合理运用．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
如图，已知棱长为1的正方体中ABCD-A1B1C1D1中，P，Q是面对角线A1C1上的两个不同动点，给出以下判断：
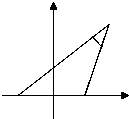设动点P到点A（-1，0）和B（1，0）的距离分别为d1和d2，∠APB=2θ，且存在常数λ（0＜λ＜1），使得d1d2sin2θ=λ（如图所示），那么点P的轨迹是（ ）| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
先后抛掷2枚均匀的一分、二分的硬币，观察落地后硬币的正、反面情况，则下列事件包含3个基本事件的是（ ）
| A、“至少一枚硬币正面向上” |
| B、“只有一枚硬币正面向上” |
| C、“两枚硬币都是正面向上” |
| D、“两枚硬币一枚正面向上，另一枚反面向上” |
偶函数y=f（x）在区间[-4，0]上单调递增，则有（ ）
A、f（-1）＞f（
| ||
B、f（
| ||
C、f（-π）＞f（-1）＞f（
| ||
D、f（-1）＞f（-π）＞f（
|
sin300°+tan240°的值是（ ）
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|