题目内容
16.命题“?x∈R,|x|+x≥0”的否定是?x∈R,|x|+x<0.分析 由已知中的原命题,结合全称命题否定的定义,可得答案.
解答 解:命题“?x∈R,|x|+x≥0”的否定是“?x∈R,|x|+x<0”,
故答案为:?x∈R,|x|+x<0.
点评 本题考查的知识点是全称命题的否定,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知随机变量X~N(6,1),且P(5<X<7)=a,P(4<X<8)=b,则P(4<X<7)=( )
| A. | $\frac{b-a}{2}$ | B. | $\frac{b+a}{2}$ | C. | $\frac{1-b}{2}$ | D. | $\frac{1-a}{2}$ |
11.已知抛物线y2=2px(p>0)上的点A到焦点F距离为4,若在y轴上存点B(0,2)使得$\overrightarrow{BA}$$•\overrightarrow{BF}$=0,则该抛物线的方程为( )
| A. | y2=8x | B. | y2=6x | C. | y2=4x | D. | y2=2x |
1.一个几何体的三视图如图所示,则其表面积为( )
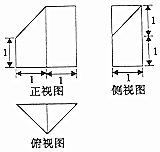

| A. | $\frac{9}{2}$+4$\sqrt{2}$ | B. | 5$+4\sqrt{2}$ | C. | 6$+4\sqrt{2}$ | D. | $\frac{13}{2}$$+4\sqrt{2}$ |
8.关于x的方程($\frac{1}{3}$)|x|+a-1=0有解,则a的取值范围是( )
| A. | 0≤a<1 | B. | -1<a≤0 | C. | a≥1 | D. | a>0 |
5.已知F1,F2是椭圆$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{4}$=1的两个焦点,经过点F2的直线交椭圆于A,B两点,若|AB|=4,则|AF1|+|BF1|=( )
| A. | 12 | B. | 9 | C. | 8 | D. | 2 |
6.方程log5x-sin2x=0的根的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
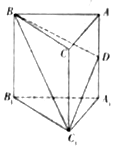 如图所示,在直三棱柱ABC-A1B1C1中,AB=AC=5,BB1=BC=8,D是AA1的中点
如图所示,在直三棱柱ABC-A1B1C1中,AB=AC=5,BB1=BC=8,D是AA1的中点