Question

1．一个几何体的三视图如图所示，则其表面积为（　　）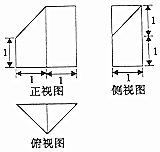

• A． $\frac{9}{2}$+4$\sqrt{2}$
• B． 5$+4\sqrt{2}$
• C． 6$+4\sqrt{2}$
• D． $\frac{13}{2}$$+4\sqrt{2}$

Answer 1

分析 由已知中的三视图，画出几何体的直观图，进而可得几何体的表面积．

解答 解：由已知中的三视图，可得该几何体的直观图如下所示：

这是一个三棱柱，切去一个三棱锥所得的组合体，
故表面积S=[2×$\frac{1}{2}$×2×1+（2+2$\sqrt{{1}^{2}+{1}^{2}}$）×2]-（2×$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×$\sqrt{2}$）+$\frac{1}{2}$×1×$\sqrt{2}$=5$+4\sqrt{2}$，
故选：B

点评 本题考查的知识点是棱柱的体积和表面积，棱锥的体积和表面积，简单几何体的三视图，难度中档．