题目内容
2.已知函数$f(x)=a-\frac{2}{{{2^x}+1}}$为R上的奇函数,则a的值为( )| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 1 | D. | -1 |
分析 根据函数奇偶性的性质,利用f(0)=0,进行求解即可.
解答 解:函数f(x)的定义域为(-∞,+∞),
若f(x)是奇函数,则f(0)=0,
即f(0)=a-$\frac{2}{1+1}$=a-1=0,
得a=1,
故选:C.
点评 本题主要考查函数奇偶性的应用,利用性质f(0)=0是解决本题的关键.

练习册系列答案
相关题目
10.已知f(x)=$\frac{{{x^2}-1}}{x+1}$,则f(f(-2))=( )
| A. | 2 | B. | 0 | C. | -2 | D. | -4 |
11.如果$0<{log_{\frac{1}{2}}}x$$<{log_{\frac{1}{2}}}y$,那么( )
| A. | 0<y<x<1 | B. | 0<x<y<1 | C. | y>x>1 | D. | x>y>1 |
12.下列各组函数相等的是( )
| A. | $f(x)=\frac{{{x^2}-1}}{x-1}与g(x)=x+1$ | B. | $f(x)=1与g(x)=\frac{{\sqrt{x^2}}}{x}$ | ||
| C. | f(x)=(x-2)0与g(x)=1 | D. | $f(x)=\sqrt{x^4}与g(x)={x^2}$ |
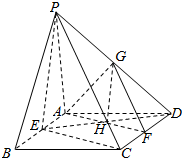 如图,四棱锥P-ABCD的底面是平行四边形,PA=PB=AB=2,E,F分别是AB,CD的中点,平面AGF∥平面PEC,PD∩平面AGF=G,ED与AF相交于点H,则GH=$\frac{\sqrt{3}}{2}$.
如图,四棱锥P-ABCD的底面是平行四边形,PA=PB=AB=2,E,F分别是AB,CD的中点,平面AGF∥平面PEC,PD∩平面AGF=G,ED与AF相交于点H,则GH=$\frac{\sqrt{3}}{2}$. 已知函数f(x)=|2x-1|.
已知函数f(x)=|2x-1|.