题目内容
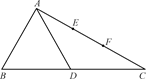
(本小题满分12分)如图,三棱柱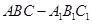 中,侧棱
中,侧棱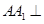 平面
平面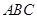 ,
,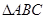 为等腰直角三角形,
为等腰直角三角形,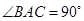 ,且
,且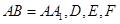 分别是
分别是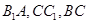 的中点.
的中点.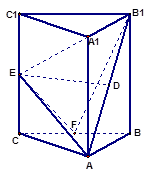
(1)求证: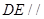 平面
平面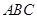 ;
;
(2)求证: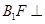 平面
平面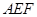 ;
;
(3)设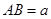 ,求三棱锥
,求三棱锥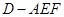 的体积.
的体积.
(1)详见解析,(2)详见解析,(3)
解析试题分析:(1)证明线面平行,关键在于找出线线平行.显然DE与三角形ABC三条边都不平行,因此需作辅助线.因为D,E都是中点,所以取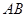 中点
中点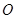 ,连接
,连接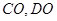 ,可证得四边形
,可证得四边形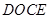 是平行四边形.因而有
是平行四边形.因而有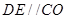 ,再根据线面平行判定定理就可证得.(2)要证明
,再根据线面平行判定定理就可证得.(2)要证明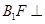 平面
平面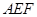 ,需证明
,需证明 及
及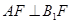 ,前面在平面中证明,利用勾股定理,即通过计算设
,前面在平面中证明,利用勾股定理,即通过计算设 ,则
,则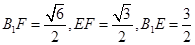 .∴
.∴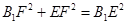 ,∴
,∴ .后者通过线面垂直与线线垂直的转化得,即由面
.后者通过线面垂直与线线垂直的转化得,即由面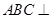 面
面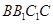 ,得
,得 面
面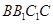 ,再得
,再得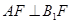 .(3)求三棱锥
.(3)求三棱锥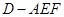 的体积关键在于求高.由(2)得
的体积关键在于求高.由(2)得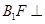 平面
平面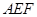 ,所以三棱锥
,所以三棱锥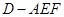 的高为
的高为 的一半,因此三棱锥
的一半,因此三棱锥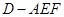 的体积为
的体积为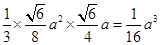 .
.
试题解析:(1)取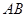 中点
中点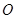 ,连接
,连接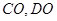 ,
,
∵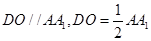 ,∴
,∴ .
.
∴四边形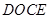 是平行四边形.
是平行四边形.
∴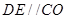 ,又∵
,又∵ ,
,
∴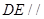 平面
平面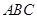 . 4分
. 4分
(2)∵ 是等腰直角三角形
是等腰直角三角形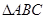 斜边
斜边 的中点,∴
的中点,∴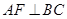 .
.
又∵三棱柱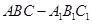 是直三棱柱,∴面
是直三棱柱,∴面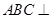 面
面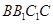 .
.
∴ 面
面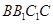 ,∴
,∴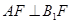 .
.
设 ,则
,则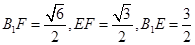 .
.
∴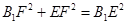 . ∴
. ∴ .
.
又 ,∴
,∴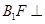 平面
平面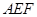 . 8分
. 8分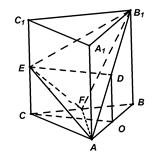
(3)∵点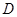 是线段
是线段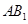 的中点,∴点
的中点,∴点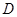 到平面
到平面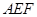 的距离是点
的距离是点 到平面
到平面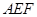 距离的
距离的 .
.
而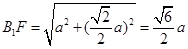 ,∴三棱锥
,∴三棱锥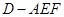 的高为
的高为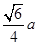 ;在
;在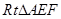 中,
中,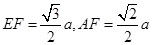 ,所以三棱锥
,所以三棱锥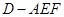 的底面面积为
的底面面积为 ,故三棱锥
,故三棱锥
练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
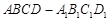 的棱长为
的棱长为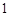 .
. 的左视图的面积;
的左视图的面积;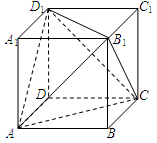
 中,底面
中,底面 为正方形,
为正方形,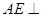 平面
平面 ,已知
,已知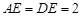 ,
,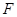 为线段
为线段 的中点.
的中点.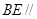 平面
平面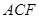 ;
;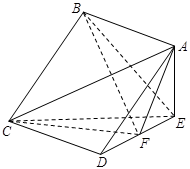
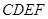 为正方形,四边形
为正方形,四边形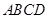 为等腰梯形,
为等腰梯形,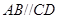 ,
,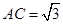 ,
,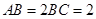 ,
,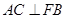 .
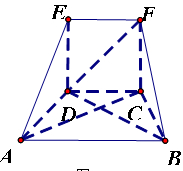
.
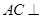 平面
平面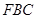 ;
;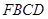 的体积;
的体积; 上是否存在点
上是否存在点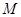 ,使
,使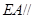 平面
平面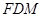 ?请证明你的结论.
?请证明你的结论.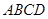 的边长为3,
的边长为3,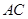 与
与 交于
交于 ,且
,且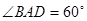 .将菱形
.将菱形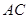 折起得到三棱锥
折起得到三棱锥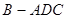 (如图),点
(如图),点 是棱
是棱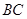 的中点,
的中点, .
.

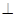 平面
平面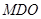 ;
;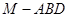 的体积.
的体积.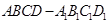 中,
中,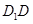
 底面
底面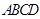 ,
,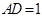 ,
,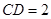 ,
, .
.
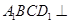 平面
平面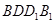 ;
;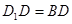 ,求四棱锥
,求四棱锥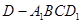 的体积.
的体积. 与
与 都是边长为
都是边长为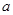 的正方形,点
的正方形,点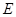 是
是 的中点,
的中点, 平面
平面
 平面
平面 ;
; 的体积.
的体积.