题目内容
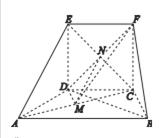
在如图所示的几何体中,四边形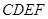 为正方形,四边形
为正方形,四边形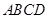 为等腰梯形,
为等腰梯形,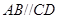 ,
,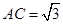 ,
,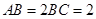 ,
,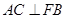 .
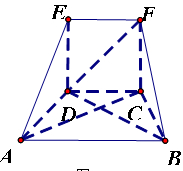
.
(1)求证: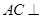 平面
平面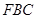 ;
;
(2)求四面体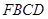 的体积;
的体积;
(3)线段 上是否存在点
上是否存在点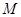 ,使
,使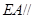 平面
平面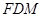 ?请证明你的结论.
?请证明你的结论.
(1)详见解析;(2)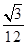 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)利用勾股定理得到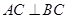 ,再结合
,再结合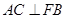 并利用直线与平面垂直的判定定理证明
并利用直线与平面垂直的判定定理证明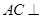 平面
平面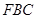 ;(2)先证明
;(2)先证明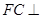 平面
平面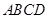 ,从而得到
,从而得到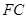 为三棱锥
为三棱锥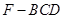 的高,并计算
的高,并计算 的面积作为三棱锥
的面积作为三棱锥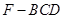 的底面积。最后利用锥体的体积公式计算四面体
的底面积。最后利用锥体的体积公式计算四面体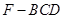 的体积;(3)连接
的体积;(3)连接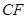 交
交 于点
于点 ,根据平行四边形的性质得到
,根据平行四边形的性质得到 为
为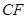 的中点,然后取
的中点,然后取 的中点
的中点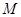 ,构造
,构造 底边的中位线
底边的中位线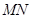 ,得到
,得到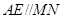 ,结合直线与平面平行的判定定理得到
,结合直线与平面平行的判定定理得到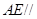 平面
平面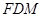 .
.
试题解析:(1)在 中,因为
中,因为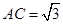 ,
,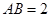 ,
,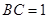 ,
,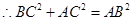 ,
,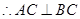 ,
,
又因为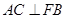 ,且
,且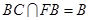 ,
, 平面
平面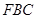 ,
,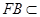 平面
平面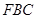 ,
,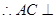 平面
平面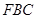 ;
;
(2)因为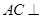 平面
平面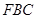 ,且
,且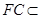 平面
平面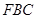 ,
,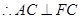 ,
,
又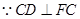 ,且
,且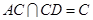 ,
,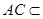 平面
平面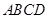 ,
,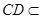 平面
平面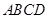 ,
,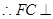 平面
平面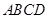 ,即
,即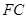 为三棱锥
为三棱锥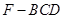 的高,
的高,
在等腰梯形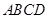 中可得
中可得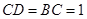 ,所以
,所以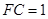 ,
,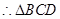 的面积为
的面积为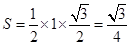 ,
,
所以四面体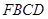 的体积为
的体积为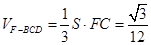 ;
;
(3)线段 上存在点
上存在点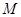 ,且
,且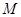 为
为 的中点时,有
的中点时,有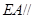 平面
平面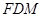 ,
,
证明如下:连接 ,
, 与
与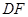 交于点
交于点 ,连接
,连接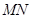 ,
, 四边形
四边形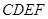 为正方形,所以
为正方形,所以

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 中,
中, 平面
平面 .
.
 平面
平面 ;
; ,
, 为
为 中点,求三棱锥
中点,求三棱锥 的体积.
的体积.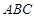 中,
中,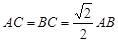 ,
,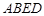 是边长为
是边长为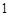 的正方形,平面
的正方形,平面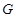 、
、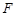 分别是
分别是 、
、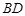 的中点.
的中点.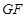 ∥底面
∥底面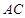 ⊥平面
⊥平面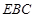 ;
; 的体积.
的体积.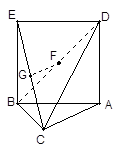
 和
和 所成的角为
所成的角为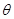 ,求
,求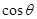 的值.
的值.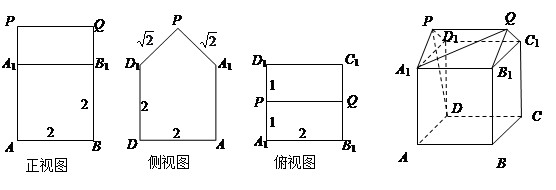
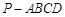 中,底面
中,底面 为矩形,
为矩形,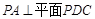 .
.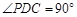 ,并指出异面直线PA与CD所成角的大小;
,并指出异面直线PA与CD所成角的大小;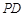 上是否存在一点
上是否存在一点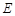 ,使得
,使得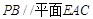 ?如果存在,求出此时三棱锥
?如果存在,求出此时三棱锥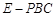 与四棱锥
与四棱锥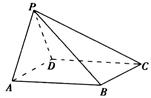
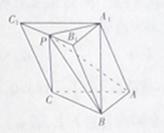
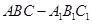 中,侧棱
中,侧棱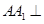 平面
平面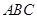 ,
,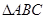 为等腰直角三角形,
为等腰直角三角形,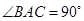 ,且
,且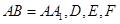 分别是
分别是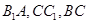 的中点.
的中点.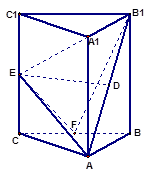
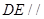 平面
平面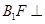 平面
平面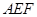 ;
;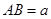 ,求三棱锥
,求三棱锥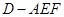 的体积.
的体积. ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.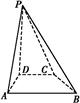
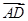 的方向相同时,画出四棱锥P
的方向相同时,画出四棱锥P