题目内容
 如图,长方体ABCD-A1B1C1D1中,ABCD是边长为1的正方形,D1B与平面ABCD所成的角为45°,则棱AA1的长为
如图,长方体ABCD-A1B1C1D1中,ABCD是边长为1的正方形,D1B与平面ABCD所成的角为45°,则棱AA1的长为考点:二面角的平面角及求法,点、线、面间的距离计算
专题:空间角
分析:连结BD,BD1,CD1,由题意知∠D1BD=45°,由此能求出棱AA1的长;由已知条件推导出∠BDC是二面角B-DD1-C的平面角,由此能求出二面角B-DD1-C的大小.
解答:
解:如图,连结BD,BD1,CD1,
∵长方体ABCD-A1B1C1D1中,
ABCD是边长为1的正方形,
D1B与平面ABCD所成的角为45°,
∴∠D1BD=45°,
∴AA1=DD1=BD=
;
∵CD⊥DD1,BD⊥DD1,
∴∠BDC是二面角B-DD1-C的平面角,
∵DC=BC,∠BCD=90°,∴∠BDC=45°,
∴二面角B-DD1-C的大小为 45°.
故答案为:
,45°.
∵长方体ABCD-A1B1C1D1中,

ABCD是边长为1的正方形,
D1B与平面ABCD所成的角为45°,
∴∠D1BD=45°,
∴AA1=DD1=BD=
| 2 |
∵CD⊥DD1,BD⊥DD1,
∴∠BDC是二面角B-DD1-C的平面角,
∵DC=BC,∠BCD=90°,∴∠BDC=45°,
∴二面角B-DD1-C的大小为 45°.
故答案为:
| 2 |
点评:本题考查长方体棱长的求法和二面角的大小的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
将一枚骰子先后掷两次,向上点数之和为x,则x≥7的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
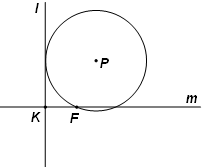 如图,已知定点F及定直线l,直线m经过F与l垂直,垂足为K,|FK|=p(p>0),动圆P经过F与l相切.
如图,已知定点F及定直线l,直线m经过F与l垂直,垂足为K,|FK|=p(p>0),动圆P经过F与l相切.