题目内容
13.若函数f(x)=x3+bx(x∈R)在点(-1,f(-1))处的切线与直线y=-x+2a平行,则实数b的值-4.分析 求出原函数的导函数,得到f′(1),由函数f(x)=x3+bx(x∈R)在点(-1,f(-1))处的切线与直线y=-x+2a平行即可求得b值.
解答 解:由f(x)=x3+bx,得f′(x)=3x2+b,
∴f′(1)=3+b,
∵函数f(x)=x3+bx(x∈R)在点(-1,f(-1))处的切线与直线y=-x+2a平行,
∴3+b=-1,解得b=-4.
故答案为:-4.
点评 本题考查利用导数研究过曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知等差数列{an}满足a2=2,点(a4,a6)在直线x+2y-16=0上.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Sn.
8.两圆x2+y2-4x+2y+1=0与x2+y2+4x-4y-1=0的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
5.在△OMN中,点A在OM上,点B在ON上,且AB∥MN,2OA=OM,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则终点P落在四边形ABNM内(含边界)时,$\frac{y+x+2}{x+1}$的取值范围是( )
| A. | $[\frac{1}{2},2]$ | B. | $[\frac{1}{3},3]$ | C. | $[\frac{3}{2},3]$ | D. | $[\frac{4}{3},4]$ |
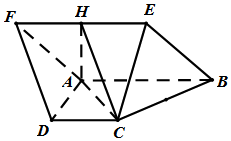 如图所示,菱形ABEF⊥直角梯形ABCD,∠BAD=∠CDA=90°,∠ABE=60°,AB=2AD=2CD=2,H是EF的中点
如图所示,菱形ABEF⊥直角梯形ABCD,∠BAD=∠CDA=90°,∠ABE=60°,AB=2AD=2CD=2,H是EF的中点