题目内容
已知函数f(x)定义域为R,则下列命题:
①若y=f(x)为偶函数,则y=f(x+2)的图象关于y轴对称.
②若y=f(x+2)为偶函数,则y=f(x)关于直线x=2对称.
③若函数y=f(2x+1)是偶函数,则y=f(2x)的图象关于直线x=
对称.
④若f(x-2)=f(2-x),则y=f(x)关于直线x=2对称.
⑤函数y=f(x-2)和y=f(2-x)的图象关于x=2对称.
其中正确的命题序号是 .
①若y=f(x)为偶函数,则y=f(x+2)的图象关于y轴对称.
②若y=f(x+2)为偶函数,则y=f(x)关于直线x=2对称.
③若函数y=f(2x+1)是偶函数,则y=f(2x)的图象关于直线x=
| 1 |
| 2 |
④若f(x-2)=f(2-x),则y=f(x)关于直线x=2对称.
⑤函数y=f(x-2)和y=f(2-x)的图象关于x=2对称.
其中正确的命题序号是
考点:命题的真假判断与应用
专题:计算题,函数的性质及应用
分析:由偶函数的图象关于y轴对称,以及图象的平移,即可判断①、②、③;
由f(a+x)=f(b-x),则函数关于x=
对称,即可判断④;
令x-2=t,则函数y=f(x-2)即y=f(t),y=f(2-x)即为y=f(-t),而函数y=f(t)和y=f(-t)关于t=0对称,即可判断⑤.
由f(a+x)=f(b-x),则函数关于x=
| a+b |
| 2 |
令x-2=t,则函数y=f(x-2)即y=f(t),y=f(2-x)即为y=f(-t),而函数y=f(t)和y=f(-t)关于t=0对称,即可判断⑤.
解答:
解:对于①,y=f(x)为偶函数,则f(x)的图象关于y轴对称,
y=f(x+2)的图象可由f(x)的图象向左平移2个单位得到,则所得图象关于x=-2对称,则①错;
对于②,若y=f(x+2)为偶函数,则f(x+2)的图象关于x=0对称,
而y=f(x)的图象可由f(x+2)的图象向右平移2个单位得到,则有关于直线x=2对称,则②对;
对于③,若函数y=f(2x+1)是偶函数,则f(2x+1)的图象关于x=0对称,
而y=f(2x)的图象可由f(2x+1)向右平移
个单位得到,则所得图象关于x=
对称,则③对;
对于④,若f(x-2)=f(2-x),即为f(x)=f(-x),则f(x)为偶函数,关于y轴对称,则④错;
对于⑤,令x-2=t,则函数y=f(x-2)即y=f(t),y=f(2-x)即为y=f(-t),
而函数y=f(t)和y=f(-t)关于t=0对称,即有函数y=f(x-2)和y=f(2-x)的图象关于x=2对称,则⑤对.
故答案为:②③⑤.
y=f(x+2)的图象可由f(x)的图象向左平移2个单位得到,则所得图象关于x=-2对称,则①错;
对于②,若y=f(x+2)为偶函数,则f(x+2)的图象关于x=0对称,
而y=f(x)的图象可由f(x+2)的图象向右平移2个单位得到,则有关于直线x=2对称,则②对;
对于③,若函数y=f(2x+1)是偶函数,则f(2x+1)的图象关于x=0对称,
而y=f(2x)的图象可由f(2x+1)向右平移
| 1 |
| 2 |
| 1 |
| 2 |
对于④,若f(x-2)=f(2-x),即为f(x)=f(-x),则f(x)为偶函数,关于y轴对称,则④错;
对于⑤,令x-2=t,则函数y=f(x-2)即y=f(t),y=f(2-x)即为y=f(-t),
而函数y=f(t)和y=f(-t)关于t=0对称,即有函数y=f(x-2)和y=f(2-x)的图象关于x=2对称,则⑤对.
故答案为:②③⑤.
点评:本题考查函数的奇偶性和对称性及运用,考查图象的平移规律,考查运算和判断、观察能力,属于基础题和易错题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
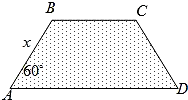 某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9
某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9| 3 |
| 3 |
| A、[3,5] |
| B、(3,5) |
| C、(2,6] |
| D、[2,6) |