题目内容
18.在△ABC中,AB=AC,cos∠ABC=$\frac{1}{3}$,若以A,B为焦点的双曲线经过点C,那么该双曲线的离心率为3.分析 先确定C在双曲线的右支上,由双曲线定义知|BD|=$\frac{1}{2}$|BC|=$\frac{1}{2}$(2c-2a)=c-a,利用cos∠ABD=$\frac{1}{3}$,即$\frac{c-a}{2c}$=$\frac{1}{3}$,即可求出双曲线的离心率.
解答 解:不妨设A、B为左、右焦点,实半轴长为a,半焦距为c,
若点C在双曲线的左支上,设BC中点为D,
由定义知|BD|=$\frac{1}{2}$|BC|=$\frac{1}{2}$(2c+2a)=c+a,
在Rt△ABD中,由cos∠ABC=$\frac{1}{3}$,
故$\frac{c+a}{2c}$=$\frac{1}{3}$,不可能;
故C在双曲线的右支上,
设BC中点为D,由双曲线定义知|BD|=$\frac{1}{2}$(2c-2a)=c-a,
在Rt△ABD中,cos∠ABD=$\frac{1}{3}$,即$\frac{c-a}{2c}$=$\frac{1}{3}$,
可得c=3a,即有e=$\frac{c}{a}$=3.
故答案为:3.
点评 本题考查双曲线的离心率,注意运用双曲线的定义和等腰三角形的性质,确定C在双曲线的右支上是关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
8.设a=0.6${\;}^{\frac{1}{2}}$,b=0.5${\;}^{\frac{1}{4}}$,c=lg0.4,则( )
| A. | a<b<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
9.R表示实数集,集合M={x|0<x<2},N={x|x2+x-6≤0},则下列结论正确的是( )
| A. | M∈N | B. | ∁RM⊆N | C. | M∈∁RN | D. | ∁RN⊆∁RM |
10.在△ABC中,如果sinA:sinB:sinC=6:7:9,则△ABC一定是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 不能确定 |
7.在数列{an}中,a1=1,且anan+1+$\sqrt{3}$(an-an+1)+1=0,则a2016=( )
| A. | 1 | B. | -1 | C. | 2+$\sqrt{3}$ | D. | 2-$\sqrt{3}$ |
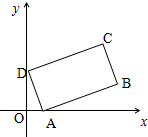 如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别位于x轴、y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}•\overrightarrow{OC}$的最大值是6.
如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别位于x轴、y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}•\overrightarrow{OC}$的最大值是6.