题目内容
8.设a=0.6${\;}^{\frac{1}{2}}$,b=0.5${\;}^{\frac{1}{4}}$,c=lg0.4,则( )| A. | a<b<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
分析 利用指数函数的性质判断a、b大小,利用对数判断c的范围,即可得到结果.
解答 解:a=0.6${\;}^{\frac{1}{2}}$,b=0.5${\;}^{\frac{1}{4}}$=$(0.{5}^{\frac{1}{2}})^{\frac{1}{2}}$,
∵0.6<$0.{5}^{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$,
∴a=0.6${\;}^{\frac{1}{2}}$<b=0.5${\;}^{\frac{1}{4}}$,而且a>0,
c=lg0.4<0,
所以c<a<b.
故选:D.
点评 本题考查函数值的大小比较,考查计算能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
18.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的实轴的两个端点和虚轴的两个端点恰好构成一个正方形,则此双曲线的离心率为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
16.设i为虚数单位,复数z=$\frac{3-i}{i}$,则z的共轭复数$\overline{z}$=( )
| A. | -1-3i | B. | 1-3i | C. | -1+3i | D. | 1+3i |
17.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的焦点且垂直于实轴的直线交双曲线的渐近线于A,B两点,已知|AB|等于虚轴长的两倍,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
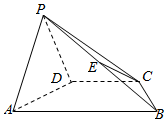 如图所示,四棱锥P-ABCD的底面是梯形,且AB∥CD,AB⊥平面PAD,E是PB中点,CD=PD=AD=$\frac{1}{2}$AB.
如图所示,四棱锥P-ABCD的底面是梯形,且AB∥CD,AB⊥平面PAD,E是PB中点,CD=PD=AD=$\frac{1}{2}$AB.