题目内容
9.R表示实数集,集合M={x|0<x<2},N={x|x2+x-6≤0},则下列结论正确的是( )| A. | M∈N | B. | ∁RM⊆N | C. | M∈∁RN | D. | ∁RN⊆∁RM |
分析 化简N={x|x2+x-6≤0}={x|-3≤x≤2},从而确定M?N;从而求得.
解答 解:∵N={x|x2+x-6≤0}={x|-3≤x≤2},
而M={x|0<x<2},
∴M?N;
∴∁RN⊆∁RM,
故选D.
点评 本题考查了集合的化简运算及集合间关系的判断,属于基础题.

练习册系列答案
相关题目
17.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的焦点且垂直于实轴的直线交双曲线的渐近线于A,B两点,已知|AB|等于虚轴长的两倍,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
4.命题“?x∈R,x2是无理数”的否定是( )
| A. | ?x∉R,x2不是无理数 | B. | ?x∈R,x2不是无理数 | ||
| C. | ?x∉R,x2不是无理数 | D. | ?x∈R,x2不是无理数 |
14.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的一条渐近线与直线3x+$\sqrt{6}$y+3=0垂直,以C的右焦点F为圆心的圆(x-c)2+y2=2与它的渐近线相切,则双曲线的焦距为( )
| A. | 4 | B. | 2 | C. | $\sqrt{5}$ | D. | $2\sqrt{5}$ |
1.复数z满足z(2-i)=|1+2i|,则z的虚部为( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}i$ | C. | 1 | D. | i |
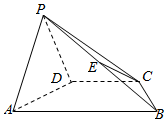 如图所示,四棱锥P-ABCD的底面是梯形,且AB∥CD,AB⊥平面PAD,E是PB中点,CD=PD=AD=$\frac{1}{2}$AB.
如图所示,四棱锥P-ABCD的底面是梯形,且AB∥CD,AB⊥平面PAD,E是PB中点,CD=PD=AD=$\frac{1}{2}$AB.