题目内容
10．在△ABC中，如果sinA：sinB：sinC=6：7：9，则△ABC一定是（ ）| A． | 钝角三角形 | B． | 直角三角形 | C． | 锐角三角形 | D． | 不能确定 |
分析 根据题意，由正弦定理分析可得a：b：c=6：7：9，进而可以设a=6k，b=7k，c=9k，进而可得c为最大边，由余弦定理计算cosC，可得cosC为负值，由三角函数的符号可得C为钝角，即可得△ABC一定是钝角三角形．
解答 解：根据题意，在△ABC中，sinA：sinB：sinC=6：7：9，则a：b：c=6：7：9，
可设a=6k，b=7k，c=9k，c为最大边，
cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=-$\frac{1}{28}$，
则C为钝角；
故△ABC一定是钝角三角形；
故选：A．
点评 本题考查利用余弦定理判定三角形的形状，涉及正弦定理的运用，解题的关键是利用正弦定理分析得到三边的关系．
练习册系列答案
相关题目
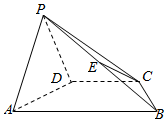如图所示，四棱锥P-ABCD的底面是梯形，且AB∥CD，AB⊥平面PAD，E是PB中点，CD=PD=AD=$\frac{1}{2}$AB．
1．复数z满足z（2-i）=|1+2i|，则z的虚部为（ ）
| A． | $\frac{{\sqrt{5}}}{5}$ | B． | $\frac{{\sqrt{5}}}{5}i$ | C． | 1 | D． | i |