题目内容
已知函数y=
sin（x+
），当y取得最小值时，tanx等于（ ）
| 2 |
| π |
| 4 |
| A、1 | ||||
| B、-1 | ||||
C、
| ||||
D、-
|
考点：正弦函数的图象
专题：计算题
分析：由正弦函数的性质，先求出当y取得最小值时x的取值从而可求tanx．
解答：
解：函数y=
sin（x+
），当y取得最小值时，有x+
=2kπ+
，故x=2kπ+
，k∈Z．
tan（2kπ+
）=1．k∈Z．
故选：A．
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 2 |
| 5π |
| 4 |
tan（2kπ+
| 5π |
| 4 |
故选：A．
点评：本题主要考察正弦函数的性质，属于基础题．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
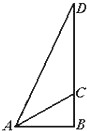如图，某城市的电视发射塔CD建在市郊的小山上，小山的高BC为30m，在地面上有一点A，测得A、C间的距离为50米，从点A观测电视发射塔的视角为45°（∠CAD=45°），求这座电视发射塔的高度．利用计算机产生0～1之间的均匀随机数a，则事件“3a-1＞0”发生的概率为（ ）
| A、0.9544 | ||
| B、0.6828 | ||
C、
| ||
D、
|
