题目内容
已知定义在[0,+∞)上的函数f(x),满足f(x)=pf(x+q),pq≠0,则称为“等比函数”,p称为“公比”,q称为“项距”.已知函数f(x)是公比为
,项距为
的“等比函数”,且x∈[0,
)时,f(x)=
,则当x∈[
n.
(n+1)](n∈N*)时,f(x)的最大值中的最小值为( )
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| -3x2+2x |
| 2 |
| 3 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
考点:抽象函数及其应用
专题:计算题,新定义,函数的性质及应用
分析:由题意得,f(x)=
f(x+
),当x∈[
,
),即有x-
∈[0,
),即可得到f(x-
),进而得到f(x)的表达式,进而求得最大值.
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:
解:由题意得,f(x)=
f(x+
),
x∈[0,
)时,f(x)=
,
当n=1时,x∈[
,
],即有x-
∈[0,
],f(x-
)=
=
=
f(x),则有f(x)=3
,
则当x=1时,取得最大值3×
=
,
当n=2,x∈[
,2],则x-
∈[0,
],
f(x-
)=
=
=
f(x-
)
=
f(x),即有f(x)=9
,则当x=
时,取得最大值9
=3
,
同理n=3,x∈[2,
],f(x)=27
,当x=
时,取得最大值9
.
故可得到,当x∈[
n.
(n+1)](n∈N*)时,f(x)的最大值为3n-1
.
故选B.
| 1 |
| 3 |
| 2 |
| 3 |
x∈[0,
| 2 |
| 3 |
| -3x2+2x |
当n=1时,x∈[
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
-3(x-
|
=
-3(x-1)2+
|
| 1 |
| 3 |
-3(x-1)2+
|
则当x=1时,取得最大值3×
| ||
| 3 |
| 3 |
当n=2,x∈[
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
f(x-
| 4 |
| 3 |
-3(x-
|
-3(x-
|
| 1 |
| 3 |
| 2 |
| 3 |
=
| 1 |
| 9 |
-3(x-
|
| 5 |
| 3 |
|
| 3 |
同理n=3,x∈[2,
| 8 |
| 3 |
|
| 7 |
| 3 |
| 3 |
故可得到,当x∈[
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
故选B.
点评:本题考查新定义及运用,考查函数的最值,考查二次函数的最值,注意对称轴和区间的关系,属于中档题.

练习册系列答案
相关题目
数列{an}的前n项和为n2,那么当n≥2时,{an}的通项公式为( )
| A、an=2n-1 | ||
| B、an=n2 | ||
C、an=
| ||
D、an=
|
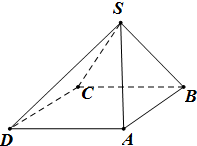 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知∠ABC=45°,AB=2,BC=2
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知∠ABC=45°,AB=2,BC=2