题目内容
函数y=x+
的值域是 .
| 3x-x2-2 |
考点:函数的值域
专题:函数的性质及应用
分析:先求的函数的定义域,根据y-x=
求得y的一个范围,进而平方消根号,整理出关于x的一元二次方程,利用二次函数的性质求得y的范围,最后综合得到答案.
| 3x-x2-2 |
解答:
解:要使函数有意义需3x-x2-2≥0,求得1≤x≤2,
y-x=
≥0,①
∴y≥x≥1,②
对①式等号两边平方得(y-x)2=3x-x2-2,
整理得2x2-(3+2y)x+2+y2=0,
令f(x)=2x2-(3+2y)x+2+y2,f(1)=y2-2y+1≥0,
要使方程2x2-(3+2y)x+2+y2=0,在[1,2]范围内有解,需
求得
<y≤
,③
综合②③得1≤y≤
,
故答案为:[1,
].
y-x=
| 3x-x2-2 |
∴y≥x≥1,②
对①式等号两边平方得(y-x)2=3x-x2-2,
整理得2x2-(3+2y)x+2+y2=0,
令f(x)=2x2-(3+2y)x+2+y2,f(1)=y2-2y+1≥0,
要使方程2x2-(3+2y)x+2+y2=0,在[1,2]范围内有解,需
|
| 1 |
| 2 |
3+
| ||
| 2 |
综合②③得1≤y≤
3+
| ||
| 2 |
故答案为:[1,
3+
| ||
| 2 |
点评:本题主要考查了函数的值域,二次函数的性质.运用了转化与化归的思想,利用二次函数的性质求值域.

练习册系列答案
相关题目
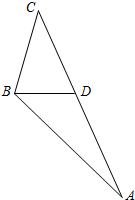 近日我渔船编队在钓鱼岛附近点A周围海域作业,在B处的海监15船测得A在其南偏东45°方向上,测得渔政船310在其北偏东15°方向上,且与B的距离为4
近日我渔船编队在钓鱼岛附近点A周围海域作业,在B处的海监15船测得A在其南偏东45°方向上,测得渔政船310在其北偏东15°方向上,且与B的距离为4